
- •1. Введение. Предмет математической физики.
- •2 . Понятие об уравнениях с частными производными первого порядка. Однородное линейное уравнение.
- •3 . Примеры.
- •Уравнение гиперболического типа.
- •1. Задача Коши. Метод распространения волн. Формула Даламбера.
- •Характеристическое направление и характеристики оператора h[f].
- •2 . Характеристическая форма оператора.
- •3. Рассмотрим систему линейных уравнений
- •Уравнения характеристик.
- •6. Решение задачи Коши для неоднородного волнового уравнения.
- •Полуограниченная прямая. Метод продолжений.
- •Решение задач на полуограниченной прямой методом продолжений.
- •Р ешение задачи Коши для двухмерного волнового уравнения. Формула Пуассона.
2 . Понятие об уравнениях с частными производными первого порядка. Однородное линейное уравнение.
Уравнение первого порядка в частных производных имеет вид: (1)
Его решением будет функция U=U(x1, x2,…, xn) (2)
Е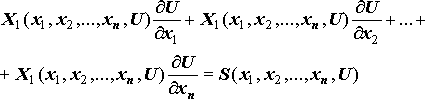 сли
в (1) Ф зависит линейно от частных
производных искомой функции, то такое
уравнение называется линейным. Его
можно записать в виде: (3)
сли
в (1) Ф зависит линейно от частных
производных искомой функции, то такое
уравнение называется линейным. Его
можно записать в виде: (3)
Если S(x1, x2,…, xn)=0, то (3) – линейное однородное уравнение с частными производными. Такое уравнение имеет решение вида:
U=c,(c=const), (7)
Которое называется очевидным.
Наряду с уравнением (3) при S=0, рассмотрим систему уравнений (обыкновенную) в симметрической форме:(5)
О![]() на
называется соответствующей линейному
однородному уравнению с частными
производными.
на
называется соответствующей линейному
однородному уравнению с частными
производными.
Предположим, что его коэффициенты X1, X2,…, Xn непрерывно дифференцируемы в некоторой окрестности точки (x1(0), x2(0),…, xn(0)) и кроме того не обращаются в нуль в этой точке. Будем считать Xn(x1(0), x2(0),…, xn(0))¹0.
При сделанных предположениях однородное уравнение имеет семейство решений, содержащее произвольную функцию. Это семейство решений может быть найдено следующим образом.
Система (5) имеет (n-1) независимых интегралов y1(xi), y2(xi), …,yn-1(xi), i=1..n-1, определённых в некоторой окрестности точки (x1(0), x2(0),…, xn(0)).
Любая
непрерывная функция от них
(![]() 7)
7)
б![]() удет
интегралом системы (5) и, следовательно,
решением системы (5) при S=0. Таким образом,
(3) имеет семейство решений
удет
интегралом системы (5) и, следовательно,
решением системы (5) при S=0. Таким образом,
(3) имеет семейство решений
Это семейство, зависящее от функции F, называется общим решением однородного линейного уравнения в частных производных первого порядка.
В случае двух независимых переменных имеем:(8)
С![]()
![]() оответствующая
система вырождается в одно дифференциальное
уравнение: (9)
оответствующая
система вырождается в одно дифференциальное
уравнение: (9)
Если y(x,y) есть интеграл этого уравнения, то общим решением (8) будет
z=F[y(x,y)] (10), где F(y)- произвольная непрерывно дифференцируемая функция от y. Если рассматривать x,y,z как прямоугольные координаты точки трёхмерного пространства, то решению z=z(x,y) уравнения (8) соответствует некоторая поверхность. Эта поверхность называется интегральной поверхностью (8).
Пример.
![]()
То есть общее решение имеет вид
z=F(y), z=F(x2+y2) и представляет собой поверхность вращения с осью OZ. Интегральными поверхностями этого уравнения являются поверхности вращения z=F(x2+y2).
В частности, при
1) F(y)=y получаем z=x2+y2-параболоид вращения;
2) F(y)=(R2-y)1/2Þz=(R2-x2-y2)1/2-сферическая поверхность;
3) F(y)=(y)1/2Þ z=(x2+y2)1/2- конус;
4) F(y)=С- плоскость.
3 . Примеры.
1. Найти общее решение уравнения:
и выделить решение, удовлетворяющее начальному условию: z=2y при х=0.
о![]() бщее
решение z=F(x2-y2).
бщее
решение z=F(x2-y2).
Р![]() ешаем
задачу Коши:
ешаем
задачу Коши:
.
И![]() скомое
решение: z=2y=2(-y)1/2;Þz=2(y2-x2)1/2
скомое
решение: z=2y=2(-y)1/2;Þz=2(y2-x2)1/2
2. ; (*)
Система (*) имеет независимые интегралы
о![]() бщее
решение Þ U=F(y/x, z2/x)
бщее
решение Þ U=F(y/x, z2/x)
3![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- общее решение.
Р![]() ешаем
задачу Коши:
ешаем
задачу Коши:
U
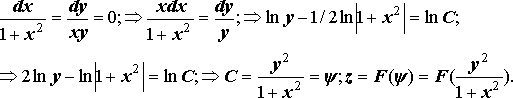 =lnz-x/y-
частное решение.
=lnz-x/y-
частное решение.
Р![]() ешаем
задачу Коши:
ешаем
задачу Коши:
#2
Классификация линейных дифференциальных уравнений с частными производными второго порядка на плоскости. Характеристики.
Всякое уравнение, связывающее между собой искомую функцию U(x1, x2,…, xn), независимые переменные x1, x2,…, xn и её производные, называется дифференциальным уравнением в частных производных.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение. Всякая функция U(x1, x2,…, xn), удовлетворяющая уравнению, называется его решением.
К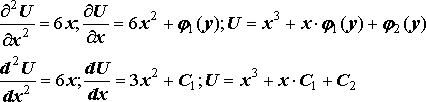 ак
и обыкновенное дифференциальное
уравнение, уравнение в частных производных
имеет бесчисленное множество решений.
Если для обыкновенного дифференциального
уравнения решение зависит от произвольных
постоянных, для уравнения в частных
производных решение зависит от
произвольных функций.
ак
и обыкновенное дифференциальное
уравнение, уравнение в частных производных
имеет бесчисленное множество решений.
Если для обыкновенного дифференциального
уравнения решение зависит от произвольных
постоянных, для уравнения в частных
производных решение зависит от
произвольных функций.
Пример.
Уравнение
второго порядка имеет вид:(![]() 1)
1)
У![]() равнение
называется линейным относительно
старших производных, если оно имеет
вид:(2)
равнение
называется линейным относительно
старших производных, если оно имеет
вид:(2)
где a11, a12, a22, являются функциями x и y.
Если же a11, a12, a22, зависят от U, Ux, Uy, то уравнение называется квазилинейным.
У![]() равнение
называется линейным, если оно линейно
как относительно старших производных
Uхх, Uxy, Uyy, так и
относительно функции U и её первых
производных.(3)
равнение
называется линейным, если оно линейно
как относительно старших производных
Uхх, Uxy, Uyy, так и
относительно функции U и её первых
производных.(3)
a11, a12, a22,b1,b2,c,f- функции x и y. Если f(x,y)=0, то (3)- однородное уравнение.
С помощью
преобразования переменных,![]() (4)
(4)
допускающего обратное преобразование, получим новое уравнение, равносильное исходному. Выберем x и h, чтобы уравнение в этих переменных имело наиболее простую форму (то есть чтобы максимальное число коэффициентов при Uxx, Uxy, Uyy обратились в нуль).
П![]() усть
функции (4) непрерывны вместе со своими
частными производными в рассматриваемой
области и якобиан (5)
усть
функции (4) непрерывны вместе со своими
частными производными в рассматриваемой
области и якобиан (5)
У
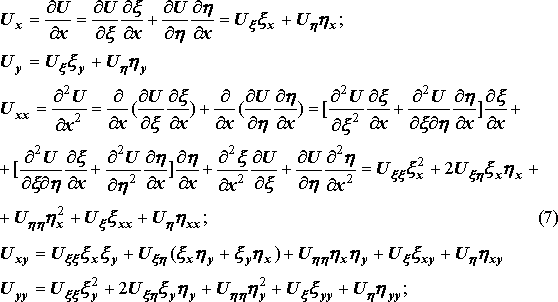 словие
обеспечивает существование обратного
преобразования.Осуществим теперь замену
переменных. При этом U(x,y) заменится на
U(x,h), в которой новые переменные x, h
связаны с x, y соотношением вида: (6)
словие
обеспечивает существование обратного
преобразования.Осуществим теперь замену
переменных. При этом U(x,y) заменится на
U(x,h), в которой новые переменные x, h
связаны с x, y соотношением вида: (6)
П![]()
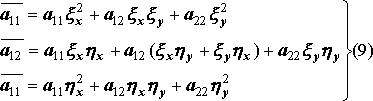 одставляя
(7) в (3), получаем: (8)
одставляя
(7) в (3), получаем: (8)
Выберем переменные h и x так, чтобы коэффициент был бы равен нулю. Из первого соотношения (9) видно, что этот вопрос эквивалентен вопросу разрешимости следующего дифференциального уравнения относительно функции z=j(x,y): (10)
Д![]()
![]() окажем
лемму: если z=j(x,y) является частным
решением уравнения (10), то соотношение
j(x,y)=С представляет собой общий интеграл
обыкновенного дифференциального
уравнения:(11)
окажем
лемму: если z=j(x,y) является частным
решением уравнения (10), то соотношение
j(x,y)=С представляет собой общий интеграл
обыкновенного дифференциального
уравнения:(11)
Доказательство.
Пусть z=j(x,y) есть решение (10). Тогда zx=jx, zy=jy; zx/zy=jx/jy, и, следовательно, верно такое тождество:(12)
Е![]() сли
соотношение j(x,y)=С определяет y как
функцию х, то y’=dy/dx=-jx/jy
(производная неявной функции). Отсюда
следует, что y=j(x,C) удовлетворяет уравнению
(11), так как(13)
сли
соотношение j(x,y)=С определяет y как
функцию х, то y’=dy/dx=-jx/jy
(производная неявной функции). Отсюда
следует, что y=j(x,C) удовлетворяет уравнению
(11), так как(13)
а![]() ,
следовательно, функция j(x,y)=С есть
интеграл (11).
,
следовательно, функция j(x,y)=С есть
интеграл (11).
Для доказательства обратной леммы все рассуждения нужно повторить в обратном порядке.
Рассмотрим некоторую точку M0(x0,y0) некоторой кривой j(x,y)=С и докажем, что для этой точки уравнение (10) выполняется. Покажем, что это соотношение имеет место для точки M0(x0,y0) и для всех точек из области существования.
И з (13) следует, что для точки M0(x0,y0)
,
т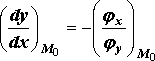 ак
как
ак
как
О![]() тсюда
следует
тсюда
следует
то есть z=j(x,y)- решение уравнения (10).
Это соотношение справедливо для всех точек области, так как точка М0- произвольная из этой области. Отсюда следует: чтобы найти два частных решения уравнения (10) требуется найти общий интеграл обыкновенного дифференциального уравнения (11).
Полагая x=j(x,y), где j(x,y)=const есть общий интеграл уравнения (11), мы обращаем в нуль коэффициент при Uxx. Если y(x,y)=const- другой интеграл (11), то, полагая h=y(x,y)=const, мы обратим в нуль коэффициент при Uhh.
Уравнение (11) называется характеристическим уравнением для уравнения (3), а его интегралы- характеристиками уравнения (3).
И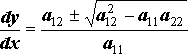 з
(11) следует (14)
з
(11) следует (14)
![]()
Знак определяет тип уравнения:
1![]() )
- уравнение гиперболического
типа;
)
- уравнение гиперболического
типа;
2![]() )
- уравнение параболического
типа;
)
- уравнение параболического
типа;
3![]() )
- уравнение эллиптического
типа.
)
- уравнение эллиптического
типа.
П риведение уравнений второго порядка в частных производных к каноническому виду.
I . 1) ; то даёт два семейства характеристик.
j![]() (x,y)=С1;
y(x,y)=С2. Если положить x=j(x,y), h=y(x,y),
то (по доказанной лемме) и уравнение (8)
примет вид:
(x,y)=С1;
y(x,y)=С2. Если положить x=j(x,y), h=y(x,y),
то (по доказанной лемме) и уравнение (8)
примет вид:
- первая каноническая форма уравнения гиперболического типа или
![]()
2![]()
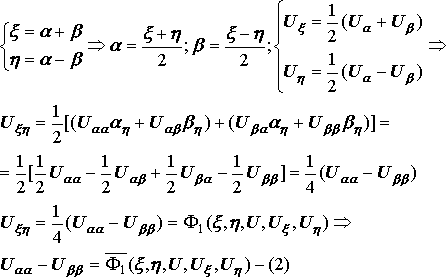 )
(1)
)
(1)
(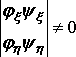 2)-
вторая каноническая форма уравнения
гиперболического типа.
2)-
вторая каноническая форма уравнения
гиперболического типа.
I![]()
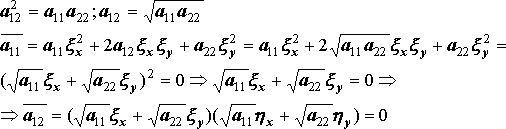
![]() I.
, то имеется только одна характеристика,
положив x=j(x,y), h- произвольная, ,
получим . Но так
как ; то
I.
, то имеется только одна характеристика,
положив x=j(x,y), h- произвольная, ,
получим . Но так
как ; то
П![]() оэтому
уравнение примет вид:
оэтому
уравнение примет вид:
- каноническая форма для уравнения параболического типа.
I II. . В правой части будут комплексные функции и уравнение распадается на два дифференциальных уравнения, интегралы которых j(x,y)=С1 и y(x,y)=С2 есть комплексно-сопряжённые функции. Преобразуем уравнение (1) по формулам: x=j(x,y), h=y(x,y). В этом случае
![]() и
уравнение примет вид как и в первом
случае:
и
уравнение примет вид как и в первом
случае:
![]()
т![]() олько
x и h будут комплексными переменные.
Выгодно ввести новые действительные
переменные a, b:
олько
x и h будут комплексными переменные.
Выгодно ввести новые действительные
переменные a, b:
![]()
Тогда
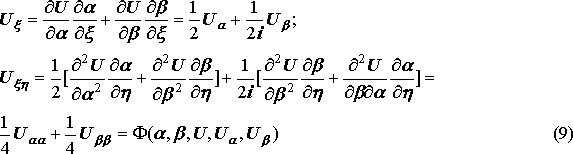
Линейные уравнения с постоянными коэффициентами.
К![]() анонические
формы линейных уравнений имеют вид:
анонические
формы линейных уравнений имеют вид:
; (1)- гиперболическое
![]()
![]()
; (3)- параболическое.
И![]() ли
ли
![]()
![]() ;
(1’)
;
(1’)
; (2’)
; (3’)
Если исходное уравнение было линейным с постоянными коэффициентами, то в канонических уравнениях a, b, g будут постоянными. В этом случае уравнения (1’)-(3’) допускают дальнейшее упрощение при помощи замены искомой функции по формуле:(4)
г![]() де
m, n- числа, подлежащие определению.
де
m, n- числа, подлежащие определению.
В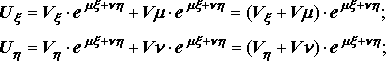 ычислим
производные функции U:(5)
ычислим
производные функции U:(5)
И так далее.
Из уравнения (1’) следует, что
е![]() сли
положить m=-b; n=-a, то Vxh+g1V=f1(x,h),
где g1=g-ab;
сли
положить m=-b; n=-a, то Vxh+g1V=f1(x,h),
где g1=g-ab;
А![]() налогично
для уравнения эллиптического и
параболического типов получим:(7)
налогично
для уравнения эллиптического и
параболического типов получим:(7)
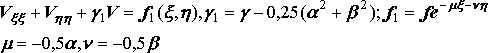
(8)
4![]() .
Классические уравнения математической
физики и их физическая интерпретация.
.
Классические уравнения математической
физики и их физическая интерпретация.
Уравнение |
Математическая форма |
Физическая интерпретация |
Л |
|
Установившееся течение жидкости. Стационарные тепловые поля. |
П |
|
Теплопередача с внутренними источниками тепла |
Диффузии |
|
Нестационарная теплопроводность Нестационарная диффузия. |
Б |
|
Деформация пластин. |
В |
|
Распространение звуковых волн. Распространение электромагнитных волн в вакууме |
Шредингера |
m- масса частицы, h- постоянная Планка, U-потенциальная энергия, Е- полная энергия частицы,y- волновая функция. |
Основное дифференциальное уравнение квантовой механики. |
Д |
|
Переменное электромагнитное поле в потенциалах. |
#3

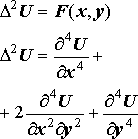 игармоническое
игармоническое