Лекции по физике «Оптика» Дисперсия света

Дисперсией света называются явления обусловленные зависимостью показателя преломления вещества от длины световой волны, т.е. n = n(λ).

У прозрачных веществ примерный вид зависимости изображен на следующем рисунке:

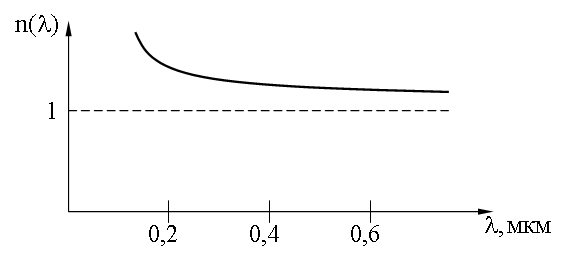
Такая зависимость n(λ), когда n уменьшается с ростом λ называется нормальной дисперсией. При прохождении белого света через призму свет разлагается в дисперсионный (призматический) спектр. Это явление впервые наблюдал И. Ньютон (1672 г.). Схема его опыта изображена на рисунке:

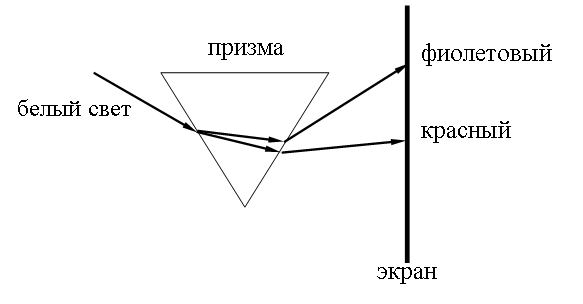
Последовательное описание взаимодействия света с веществом возможно только в рамках квантовой теории. Однако, во многих случаях можно ограничиться описанием в рамках волновой (электромагнитной) теории излучения и классической электронной теории, согласно которой каждую молекулу среды можно рассматривать как систему зарядов, имеющих возможность совершать гармонические колебания - как систему осцилляторов с различными собственными частотами и коэффициентами затухания. Движение этих осцилляторов можно рассматривать на основе законов Ньютона. Лорентц показал, что для объяснения многих оптических явлений достаточно ограничится гипотезой о существовании внутри атомов электронов, связанных квазиупруго.

В классической теории Г.А. Лорентца строение колеблющейся системы – атомов и молекул – и их колебания описываются на основе классических представлений о движении и законов Ньютона. все электроны, входящие в атом, можно разделить на оптические и электроны внутренних оболочек. На излучение и поглощение света в оптической области спектра оказывают влияние практически одни только оптические электроны. Собственные частоты электронов внутренних оболочек на столько велики, что их колебания в поле световой волны практически не возбуждаются. Поэтому в теории дисперсии можно ограничится рассмотрением только оптических электронов.

Для простоты предположим, что в атоме есть только один оптический электрон. В классической теории дисперсии оптический электрон рассматривается как затухающий гармонический осциллятор, колебания которого в поле световой волны описываются уравнением:

,

где - масса, - заряд, электрона, - квазиупругая возвращающая сила, стремящаяся вернуть электрон в положение равновесия, - сила, аналогичная силе трения и введенная для учета поглощения света, - напряженность электрического поля, действующего на электрон. Разделив все на приведем предыдущее к следующему виду:

(1)

В классической теории дисперсии оптический электрон в атоме рассматривается как затухающий дипольный осциллятор, характеризуемый определенной собственной частотой и постоянной затухания , так что в поле световой волны уравнение его движения имеет вид (1).

Несмотря на то, что с позиции современной физики применение законов классической физики к описанию движения электронов в атоме является неоправданным, такой подход приводит к результатам аналогичным тем, которые получаются гармонического осциллятора в квантовой теории дисперсии. Сама модель дипольного осциллятора в классической теории дисперсии в свете современных представлений о строении атома, конечно, выглядит чрезмерно упрощенной.

Входящая в уравнение (1)собственная частота атомного электрона может быть рассчитана только на основе квантовой теории атома. В рамках классической теории её следует рассматривать как формально введенную константу, которая определяет линию поглощения в спектре исследуемого вещества. Постоянная затухания, характеризующая «силу сопротивления», содержит вклад, обуславливаемый радиационным затуханием.

Для монохроматической волны решение (1) описывающее установившееся вынужденное колебания электрона, будем искать в виде:

. (2)

Амплитуду найдем, подставляя (2) в (1)

. (3)

В общем случае в правой части (3) вместо должно стоять значение средней макроскопической напряженности , входящей в уравнение Максвелла, однако в разряженных средах можно приять, что .

Индуцированный дипольный момент , поэтому:

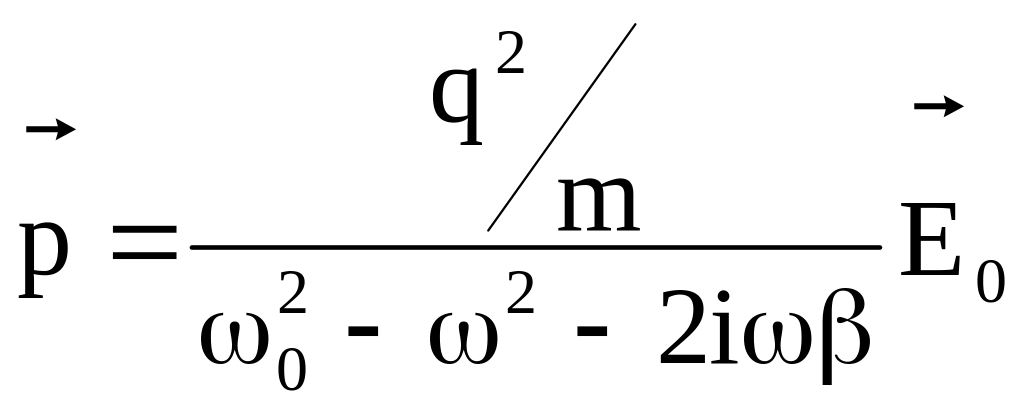. (4)

Поскольку поляризованность , где - концентрация атомов вещества (у каждого атома по одному оптическому электрону), - диэлектрическая восприимчивость, , то учитывая, что диэлектрическая проницаемость , из (4) получим:

. (5)

Из (5) следует, что является комплексной величиной:

. (6)

Введём аналогичные выражения для показателей преломлении:

, (6’)

где - комплексный показатель преломления, – показатель затухания. Используя , из (9.6), (9.6’) получим:

(7)

Выделяя реальную и мнимую части в (9.5), найдем:

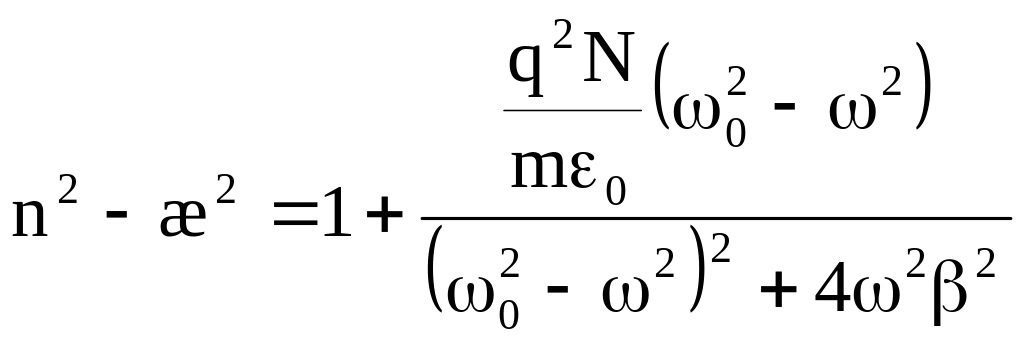, (8)

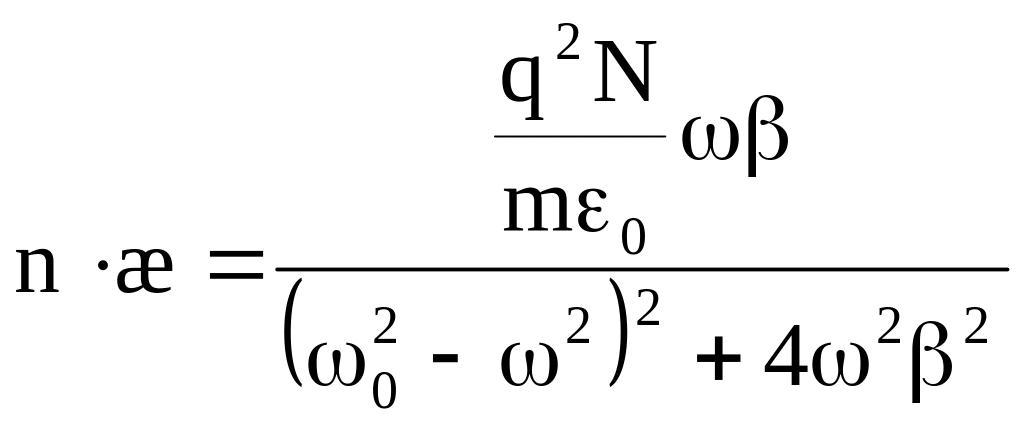(9)

При малых значение , полагая что , преобразуем (8) и (9) к виду:

, (9.8’)

. (9’)

Частотные зависимости и приведены на рис. 9. 1.

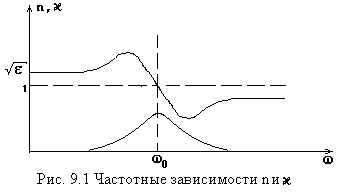
На частотах далеких от , где выполняется условие , вторым слагаемым в знаменателе (8’) можно пренебречь:

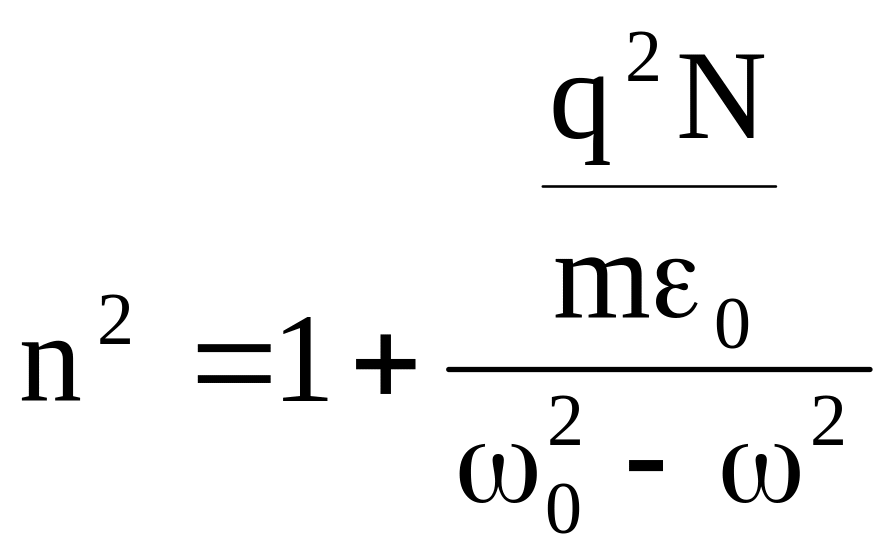. (10)

Рассматривая как малый параметр получим:

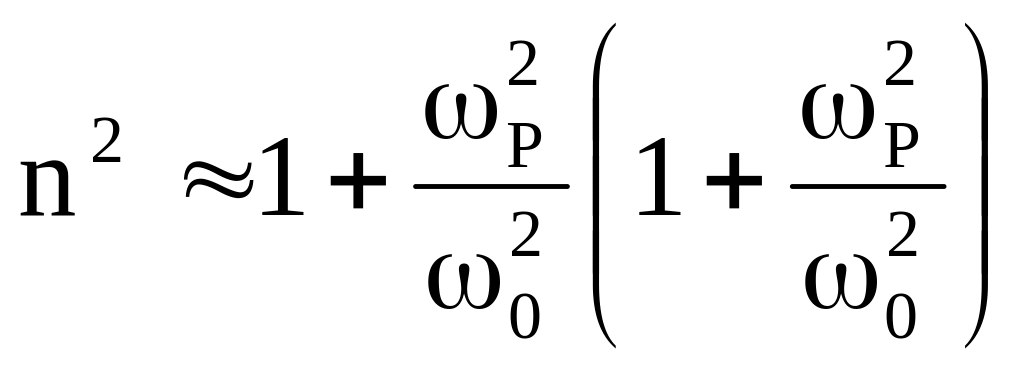, (11)

где - так называемая плазменная частота.

Переходя от частоты к длине волны (в вакууме) , получим простую формулу для сравнения с экспериментальными данными:

, (12)

где , .

Выражение с эмпирическими коэффициентами подобное (12), до появления электронной теории дисперсии было получено Френелем и Коши.

Величина дисперсии определяется производной . При дисперсию называют нормальной, при - аномальной. Из рис. 9.1 видно, что область аномальной дисперсии находится в близи . Таким образом, любое вещество, у которого , обладает областями нормальной и аномальной дисперсии.