Предел и непрерывность функции от нескольких переменных.

Будем говорить, что последовательность точек сходится при к точке , если при .

В этом случае точку называют пределом указанной последовательности и пишут: при .

Легко показать, что тогда и только тогда, когда одновременно , (т.е. сходимость последовательности точек пространства эквивалентна покоординатной сходимости).

Пусть и – предельная точка множества .

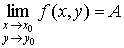Число называют пределом функции при , если для такое, что , как только . В этом случае пишут или при .

Пусть дана функция с областью определения и пусть – предельная точка множества .

Говорят, что функция непрерывна в точке , если:

1) ;

2) , т.е. .

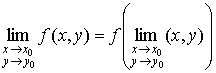Если функции и непрерывны в точке , то этим же свойством обладают функции , , а если , то и функция .

Множество называется областью, если оно: 1) является открытым множеством, т.е. содержит каждую свою точку вместе с некоторой своей -окрестностью; 2) является линейно связным множеством, т.е. для любых двух различных точек существует ломаная, соединяющая и и целиком лежащая в .

Говорят, что функция непрерывна в области , если непрерывна в каждой точке этого множества.

Частные производные. Исследование на экстремумы.

Пусть функция Z=f(M) определена в некоторой окрестности точки M(x,y) Придадим переменной x в точке M произвольное приращение Δx, оставляя значение переменной y неизменным. Тогда соответствующее приращение функции Δ_xZ=f(x+Δx,y)-f(x,y) называется частным приращением функции по переменной x в точке M(x,y). Аналогично определяется частное приращение функции по переменной y: Δ_yZ=f(x,y+Δy)-f(x,y).

Если существует предел 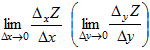, то он называется частной производной функции Z=f(M) в точке М по переменной х (по переменной у).

Из определения следует, что частная производная функции двух переменных по переменной х представляет собой обыкновенную производную функции одной переменной х при фиксированном значении переменной у. Поэтому частные производные вычисляют по формулам и правилам вычисления производных функции одной переменной.

Пример. Найти частные производные функции Z=x²-2xy²+y³

Частную производную находим как производную функции Z=f(x,y) по аргументу х в предположении, что y=const. Поэтому =(x²-2xy²+y³)'_x= =2x-2y²+0=2(x-y²)

Аналогично, =(x²-2xy²+y³)'_y=0-4xy+3y²=y(3y+4x).

Для ответа на вопрос, является ли точка области определения функции точкой экстремума, нужно использовать достаточное условие экстремума.

Пусть а вторые частные производные функции z непрерывны в некоторой окрестности точки (x₀,y₀). Введем обозначения:

Тогда, если D < 0, то в точке (x₀,y₀) экстремума нет. Если D > 0, то в точке (x₀,y₀) экстремум функции z, причем если A > 0, то минимум, а если

A < 0, то максимум. Если D = 0, то экстремум может быть, а может и не быть. В данном случае требуются дополнительные исследования