Неопределенный интеграл и основные методы интегрирования.

Неопределённый интеграл для функции — это совокупность всех первообразных данной функции.

Если функция определена и непрерывна на промежутке и — её первообразная, т.е. при , то , где С— произвольная постоянная.

Замена переменного:

Если F(x)– первообразная для f(x) на X т.е. =F(x)+C , x=j(t) дифференцируема на T и определена суперпозиция = F(j(t))+C, тогда функция F(t)=f(j(t))j¢(t) имеет первообразную, равную F(j(t)). Таким образом,

= . Для доказательства достаточно продифференцировать левую и правую части и убедиться, что получится одна и та же функция.

Примеры:

= = = , x = sin t.

J = , сделаем замену x = t6, тогда

J=6 =6 =6t – 6 arctg t + C =6 -6 arctg +C

Интегрирование по частям

Формула интегрирования по частям

Найти неопределенный интеграл.

Решение:

Используя знакомый алгоритм, интегрируем по частям:

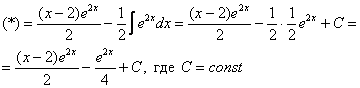
Определенный интеграл. Формула Ньютона-Лейбница.

Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю:

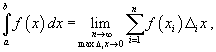где

Свойства определенного интеграла

Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b].

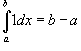
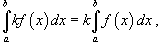где k - константа;

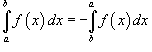
Формула Ньютона-Лейбница

Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на [a, b], то

Замена переменной в определенном интеграле

Определенный интеграл по переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):

Интегрирование по частям для определенного интеграла

В этом случае формула интегрирования по частям имеет вид:

Вычислить интеграл .

Решение. Применяя формулу Ньютона-Лейбница, получаем

 

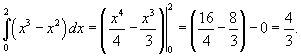
Вычислить интеграл .

Решение.

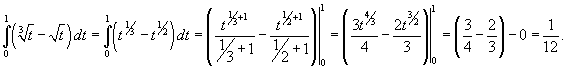
Понятие квадрируемой фигуры, кубируемого тела, спрямляемой кривой.

Пусть {S_i} - числовое множество площадей вписанных в плоскую фигуру Q многоугольников, а {S_d} - числовое множество площадей описанных вокруг фигуры Q многоугольников. Очевидно, множество {S_i} ограничено сверху (площадью любого описанного вокруг фигуры Q многоугольника), а множество {S_d} ограничено снизу (например, числом нуль). Обозначим через точную верхнюю грань множества {S_i}, а через - точную нижнюю грань множества {S_d}. Числа и называются соответственно нижней площадью и верхней площадью фигуры Q.

Плоская фигура Q называется квадрируемой, если верхняя площадь этой фигуры совпадает с ее нижней площадью . При этом число называется площадью фигуры Q. Для того чтобы плоская фигура Q была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа ε можно было указать такой описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру Q многоугольник, разность S_d - S_i площадей, которых была бы меньше ε, S_d -S_i < ε. Круг, эллипс, квадрат и т.п., являются квадрируемыми фигурами.

Пусть {V_i} - числовое множество объемов вписанных в тело многогранников, а {V_d} - числовое множество объемов описанных вокруг тела многогранников. Наименьшее из чисел, ограничивающее сверху множество {V_i} называется нижним объемом тела, а наибольшее из чисел, ограничивающее снизу множество {V_d} называется верхним объемом тела.

Если верхний объем тела совпадает с его нижним объемом , то число называется объемом тела, а само тело – кубируемым телом.

Для того чтобы тело было кубируемым, необходимо и достаточно, чтобы для любого положительного числа ε можно было указать такой описанный вокруг тела многогранник и такой вписанный в тело многогранник, разность V_d - V_i объемов, которых была бы меньше ε.

Исторически вычисление длины кривой называлось спрямлением кривой. Если длина кривой существует и конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая.

Длина кривой – это предел, к которому стремятся длины вписанных в эту кривую ломаных при неограниченном увеличении числа их звеньев.

Если плоская кривая задана в прямоугольных декартовых координатах уравнением у=f(x), где , ее длину можно вычислить по формуле .

Для параметрически заданной кривой х=х(t), y=y(t), где , ее длину можно найти по формуле .