Элементарные функции и их свойства. Операции над функциями, композиция функций, обратная функция.

Числовая последовательность и ее предел. Критерий Коши.

Числовая последовательность – функция вида y = f(x), x N, где N – множество натуральных чисел, обозначается y = f(n) или y₁, y₂,…, y_n,…. Значения y₁, y₂, y₃,… называют соответственно первым, вторым, третьим, … членами последовательности.

Последовательность - это функция, заданная на множестве натуральных чисел . Число называется пределом последовательности , если для любого положительного числа , как бы мало оно ни было, существует такой номер , что для всех c номерами справедливо неравенство .

Последовательность, предел которой - конечное число , называется сходящейся, и ее предел обозначают .

Последовательность называется фундаментальной последовательностью, если .

Если последовательность сходится, то она фундаментальна.

Доказательство: Пусть последовательность сходится: .

По определению это означает, что ,

.

Пусть m>N и n>N, тогда

.

Критерий Коши: последовательность сходится тогда и только тогда, когда она фундаментальна.

Предел и непрерывность функции в точке и на множестве.

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε>0 существует δ>0 такое, что для всех x, удовлетворяющих условию |x–a|<δ, x≠a, выполняется неравенство |f (x)–A|<ε.

Определение предела по Гейне. Число A называется пределом функции f(x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности такой, что сходящейся к числу a, соответствующая последовательность значений функции сходится к числу A.

Примеры: 1) ; 2)

Функция f(x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если

Пусть функция определена в некоторой окрестности точки a, быть может, за исключением самой точки a. Точка a называется точкой разрыва, если эта функция либо не определена в точке a, либо определена, но не является непрерывной в точке a.

Функция y=1/(x-1) разрывная в точке x₀ = 1,

Если функция непрерывна в каждой точке некоторого множества, то она называется непрерывной на этом множестве. Большинство функций, изучаемых в элементарной математике, непрерывны на всей области определения. Таковыми являются линейная функция y=kx+b, квадратичная y=ax²+bx+c, показательная и тригонометрические функции.

Непрерывность основных элементарных функций и их свойства.

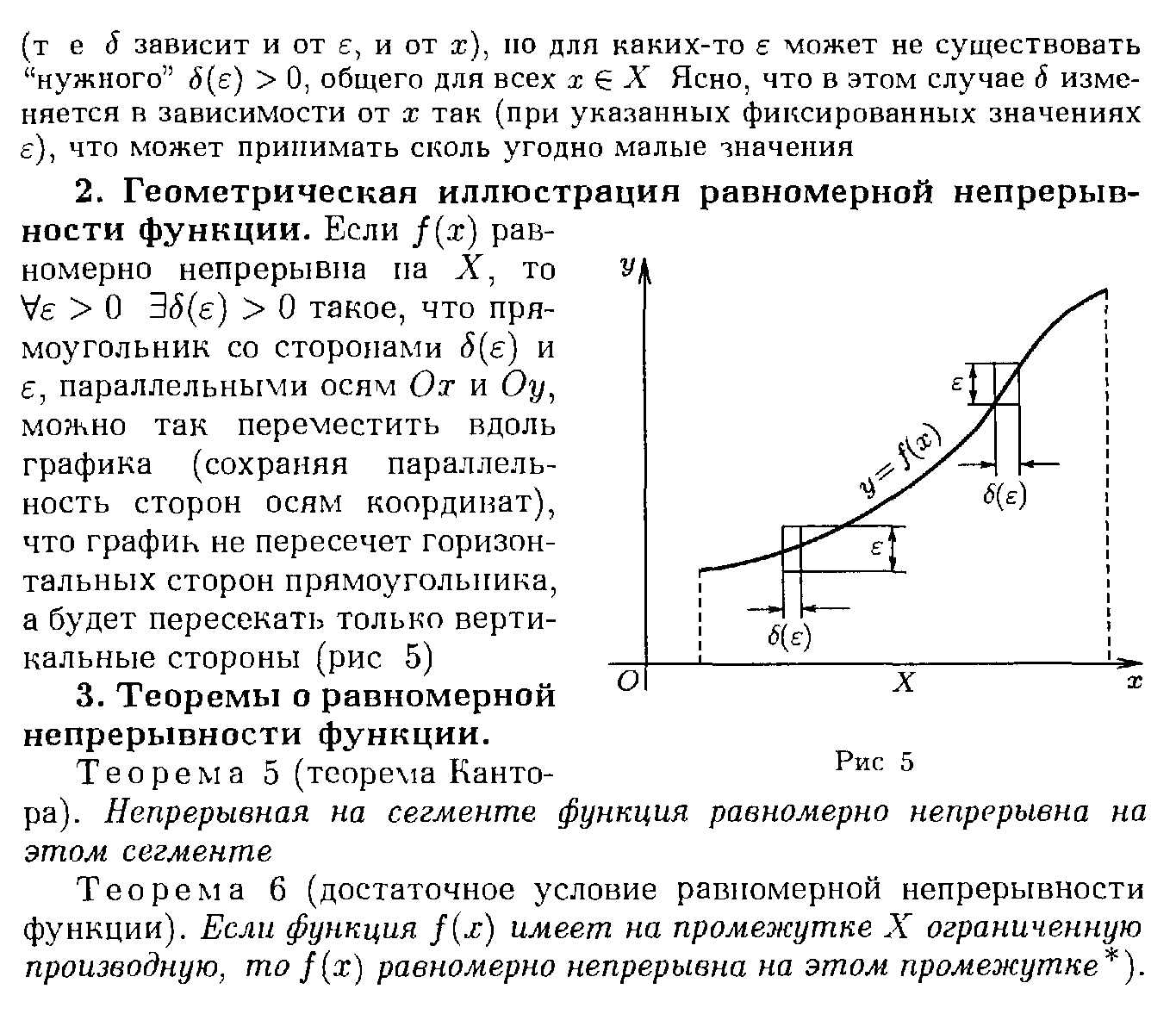
Равномерная непрерывность функции на множестве

Производная функции от одной переменной, правила дифференцирования

Дифференциал функции от одной переменной.

Дифференциал функции в точке может быть определён как линейная функция .

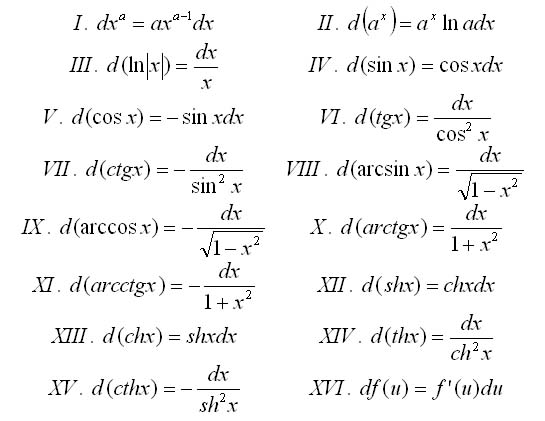
1. Дифференциал постоянной равен нулю: dc = 0, с = const.

2. Дифференциал суммы равен сумме дифференциалов слагаемых: d(u+v)=du + dv

3. Дифференциал произведения двух функций равен: d(uv) = udv + vdu.

4. Дифференциал частного u/v двух функций u=u(х) и v=v(x) определяется формулой

5. Инвариантность формы дифференциала: дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

Пусть функция u=u(x) дифференцируема в точке x₀, а функция y=f(u) дифференцируема в соответствующей точке u₀=u(x₀), тогда сложная функция y=f(u(x)) дифференцируема в точке x₀, причем df(u(x))=f ^'(u₀)u^'(x₀)dx. Так как

u^'(x₀)dx=du, то df(u(x)) = f ^'(u₀)du.

Последняя формула показывает, что дифференциал функции записывается формулой одного и того же вида как в случае функции от независимой переменной, так и в случае функции от функции. Заметим, что дифференциалы высших порядков свойством инвариантности не обладают.