8. Афинные п-мерные пространства

Если в обычном трехмерном пространстве выбрана система координат Oxyz , то каждая точка этого пространства отождествлялась с тройкой чисел -- координатами вектора . Аналогично мы можем считать, что набор из чисел является точкой -мерного пространства и рассматривать этот набор как координаты радиус-вектора этой точки. Такое -мерное пространство в отличие от векторного называется аффинным -мерным пространством. За начало координат принимается точка . За единичные векторы на осях координат в этом случае принимаются радиус-векторы точек

Любым двум точкам и аффинного пространства можно сопоставить вектор из -мерного линейного пространства. Для получения координат вектора нужно из координат конца вектора вычесть координаты начала.

Пусть точка , являющаяся началом новой системы координат, имеет координаты . Пусть  -- некоторая точка пространства с координатами в старой системе координат и в новой системе координат. Тогда связь между старыми и новыми координатами задается формулами

В трехмерном пространстве уравнение задает плоскость. Аналогично в -мерном пространстве уравнение

где  -- числа, задает плоскость размерности , обычно ее называют гиперплоскостью. В трехмерном пространстве система из двух уравнений задает прямую. В -мерном пространстве система

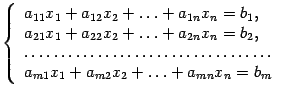из уравнений, , задает плоскость размерности , если ранг матрицы системы равен .

Если для векторов задано скалярное произведение формулой  (18.3), то в аффинном пространстве можно определять расстояние между точками. Пусть ,  -- точки пространства, тогда расстояние между ними

В соответствии с этим говорят, что уравнение задает в -мерном вещественном пространстве -мерную сферу, а неравенство

задает -мерный шар радиуса с центром в начале координат. В аффинном -мерном пространстве можно рассматривать поверхности второго порядка. Их типов оказывается тоже конечное число.

Можно рассматривать множество точек, задаваемых уравнением . При некоторых ограничениях на функцию , это уравнение будет определять -мерную поверхность (гиперповерхность), а неравенство  -- область в -мерном аффинном пространстве.

9. Евкливоды п-мерные пространства

Если координаты векторов

   и

заданы в ортонормированном базисе, то скалярное произведение вычисляется по формуле

Аналогичной формулой можно задать и скалярное произведение в -мерном пространстве.

Пусть  -- вещественное -мерное пространство, в котором задан базис . Тогда векторы и из задаются своими координатами:

Скалярное произведение векторов, обозначается оно обычно , задается формулой (1)

В отличие от обычного трехмерного пространства, где с помощью транспортира и линейки можно измерить угол между векторами и длину вектора, в -мерном пространстве ни угол между векторами, ни длину вектора измерить невозможно. Поэтому ортонормированным в -мерном пространстве называется тот базис, в котором скалярное произведение вычисляется по формуле (1).

Если ,  -- координатные столбцы векторов и , то скалярное произведение можно задать формулой

Предоставляем читателю самостоятельно убедиться в совпадении этой формулы с формулой (1)

Вещественное линейное пространство, в котором задано скалярное произведение называется евклидовым пространством.         

В трехмерном пространстве модуль вектора равен корню квадратному из скалярного произведения вектора на себя . В евклидовом пространстве модуль вектора определим аналогично

то есть

В трехмерном пространстве с помощью скалярного произведения определялся угол между векторами. В евклидовом пространстве тоже можно определить угол между векторами. Но угол в -мерном пространстве не имеет существенного значения, кроме одного случая. В трехмерном пространстве два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.

Два вектора евклидова пространства называются ортогональными, если их скалярное произведение равно нулю.         

Если  -- комплексное линейное -мерное пространство, то в нем тоже можно ввести скалярное произведение, задав его формулой

где черта над означает комплексное сопряжение.

Комплексное линейное пространство, в котором введено скалярное произведение, называется унитарным пространством.         

В унитарном пространстве модуль вектора и условие ортогональности вводятся с помощью скалярного произведения так же, как в евклидовом пространстве. В координатной записи