6. Поверхность второго порядка

Пусть в пространстве задана прямоугольная декартова система координат.

Поверхностью второго порядка называется поверхность, определяемая уравнением

(1)

где - вещественные числа, причем хотя бы одно из чисел отлично от нуля.         

1. Сфера

Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром.         

Теорема. Сфера радиуса с центром в точке имеет уравнение

2. Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид

где , , -- положительные числа.         

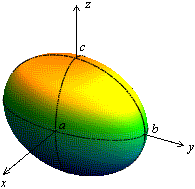
Рис. Эллипсоид

3.   Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид где , ,  -- положительные числа.   

Рис. Однополостный гиперболоид

5. Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид

где , ,  -- положительные числа.         

Рис. Изображение конуса с помощью сечений

6. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид где и -- положительные числа.         

Рис. Эллиптический параболоид

7.   Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые -- образующими.         

Рассмотрим уравнение вида

и покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси . Пусть  -- некоторая точка, координаты которой удовлетворяют уравнению. Поскольку в это уравнение не входит явно переменная , ему будут удовлетворять координаты всех точек , где  -- любое число. Следовательно, при любом точка лежит на поверхности, определяемой уравнением. Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку параллельно оси . А это означает, что поверхность, определяемая уравнением , составлена из прямых, параллельных оси , то есть она является цилиндрической поверхностью.

Заметим, что на плоскости уравнение определяет направляющую рассматриваемой цилиндрической поверхности.

Итак, делаем вывод, что если уравнение поверхности не содержит в явном виде какой-либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.

  Поверхность, которая в некоторой декартовой системе координат задается уравнением называется эллиптическим цилиндром, поверхность, которая задается уравнением называется гиперболическим цилиндром, а которая задается уравнением называется параболическим цилиндром.