18. Первая и вторая квадратичные формы кривой

Первая квадратичная форма или метрическая форма поверхности ― квадратичная форма от дифференциалов координат на поверхности, которая определяет внутреннюю геометрию поверхности в окрестности данной точки. Знание первой квадратичной формы достаточно для вычисления длин дуг, углов между кривыми, площади областей на поверхности.

Пусть поверхность задана уравнением

r = r(u,v),

где u и v ― внутренние координаты на поверхности;

dr = r_udu + r_vdv ― дифференциал радиус-вектора r вдоль выбранного направления смещения из точки M в бесконечно близкую точку M'. Квадрат главной липшицевой части приращения длины | MM' | выражается квадратом дифференциала dr:

и называется первой основной квадратичной формой поверхности. Коэффициенты первой квадратичной формы обычно обозначают через

.

или в тензорных символах

dr² = g_1,1du² + 2g_1,2dudv + g_2,2dv².

Тензор g_i,j называется основным, или метрическим, тензором поверхности.

Свойства

• Первая квадратичная форма является положительно определенной формой в обыкновенных точках поверхности:

EG − F² > 0.

Вторая квадратичная форма n-мерной поверхности, вложенной в пространство , — квадратичная форма, задающая нормальную кривизну. Пусть — нормальный вектор в точке P, а — локальная карта поверхности в точке P. Тогда вторая квадратичная форма вычисляется по формуле .

Нормальная кривизна k_n по направлению вычисляется по формуле , где g — первая квадратичная форма.

19. Внутренняя геометрия поверхности.

Пусть даны две поверхности - Ф и . Предположим, что задано непрерывное биективное отображение одной из них на другую. Такое отображение устанавливает однозначное соответствие между точками обеих поверхностей. При этом соответствии каждой кривой С на поверхности Ф отвечает некоторая кривая на поверхности и наоборот:

, .

Если при этом длина каждой кривой С равна длине соответствующей кривой , то говорят, что получается из Ф при помощи изгибания, а само отображение i называется изгибанием или изометрией (рис.1 и рис.2)

Рис.1 Рис. 2

Внутренняя геометрия поверхности изучает те свойства поверхностей и фигур на них, которые не меняются при изгибаниях. С этой точки зрения вся планиметрия представляет собой внутреннюю геометрию плоскости. Это вполне согласуется с обычным представлением, что в планиметрии изучаются свойства фигур, не меняющиеся при изометриях плоскости, т.е. наложениях.

Главным для нас будет следующий пример изгибания. Пусть поверхности Ф и . Параметризуются вектор-функциями и , заданными в одной и той же области V, пусть отображение i ставит в соответствие точке Р на поверхности Ф точку

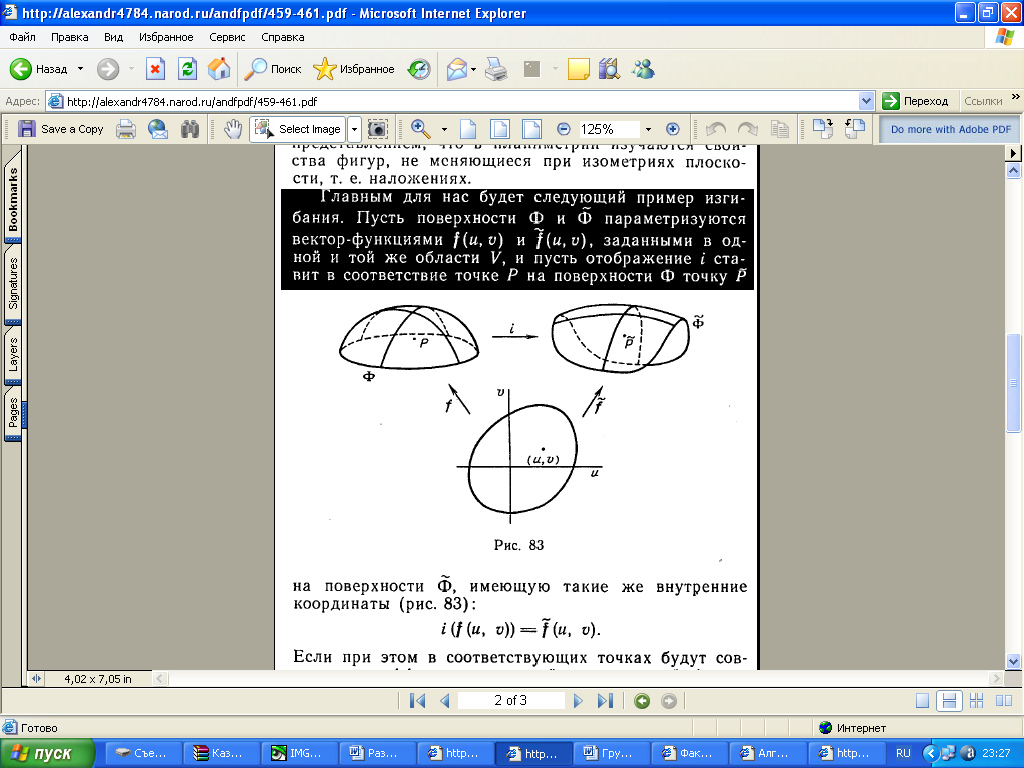
Рис.3

Н поверхности , имеющую такие же внутренние координаты (рис.3):

Если при этом в соответствующих точках будут совпадать коэффициенты первой квадратичной формы поверхностей Ф и : то, как это следует из формулы длины кривой на поверхности, отображение i будет изгибанием. Обратное утверждение верно.