14. Евклидово пространство. Процесс ортогонализации векторов

Пусть V – лин. пространство. Скалярным произведением векторов a,b  V ставит в соответствие отображение VV R, которое каждой паре векторов a,b  V ставит в соответствие действит. число (a,b), причем выполняются следующие аксиомы:

1. a*b=b*a – коммутативный закон; (a,b)=(b,a)

2. (a+b)*c=a*c+b*c – дистрибутивный закон; (a+b,c)=(a,c)+(b,c)

3. (k*a)*b=k*(a*b) или (ka,b)=k*(a,b)

4. если a0, то скалярный квадрат вектора а строго положительный (а,а)0.

Линейное пространство с определенным на нем скалярным произведением и хотя бы одним базисом называется Евклидовым пространством.

Теорема. При любом n в n-мерном линейном пространстве Vn можно определить скалярное умножение, т.е. превратить это пространство в Евклидово.

Если En – Евклидово пространство, тогда его подпространство тоже будет Евклидовым относительно скалярного произведение определенного на En.

Если En – Евклидово пространство и а1,а2, … аn есть система ненулевых векторов этого пространства, то 2 ненулевых вектора a, b  En называют ортогональными или перпендикулярными, ab, если (a,b)=0.

Если вектора образуют а1,а2, … аn образуют ортогональную систему векторов, то они линейно независимы.

Вспомним, как в обычном трехмерном пространстве мы вычисляли скалярное произведение векторов. Если координаты векторов    и были заданы в ортонормированном базисе, то скалярное произведение вычислялось по формуле ab=α₁β₁+α₂β₂+α₃β₃

Аналогичной формулой можно задать и скалярное произведение в - мерном пространстве.

Пусть  - -мерное пространство, в котором задан базис . Тогда векторы и из задаются своими координатами:

a=α₁e₁+…+α_ne_n, b=β₁e₁+…+β_ne_n

Скалярное произведение векторов, обозначается оно обычно , задается формулой

(a,b)= α₁β₁+α₂β₂+…+α_nβ_n (4)

Длиной вектора а в Евклидовом пространстве En наз. число

В трехмерном пространстве модуль вектора равен корню квадратному из скалярного произведения вектора на себя . В евклидовом пространстве модуль вектора определим аналогично то есть

|a|=

Углом между ненулевыми векторами a,b в Евклид. пространстве называется такой угол , что .

В Евклидовом пространстве - неравенство Коши-Буяковского.

Пример: Рассмотрим пространство Rn n - мерных строк с действительными коэффициентами.

Легко проверить, что в этом пространстве выполняются все свойства 1-4.

Векторы a,b называются ортогональными, если их скалярное произведение равно 0.

Нулевой вектор ортогонален любому вектору.

Система векторов называется ортогональной системой, если все векторы этой системы попарно ортогональны между собой.

Теорема. Всякая ортогональная система ненулевых векторов лин. независима.

Вектор a называется нормированным, если его скалярный квадрат равен 1, т.е. а*а=1.

Например, а(0;0;1), тогда а*а=1.

Если вектор , то а*а 0, значит нормированием вектора а называется переход к другому вектору .

Базис En называется ортонормированным, если он является ортогональной системой векторов, в которой все векторы нормированы, т.е. .

Теорема. Всякое Евклидово пространство обладает ортонормированными базисами.

Пример:

1. b1(1;1;1;1), b2(2;2;-2;-2), b3(-1/2;1/2;-1/2;1/2), b4(1;-1;-1;1) – ортогональный базис.

, .

2. Дана система векторов пространства r3. Построить ортогональную систему векторов.

а1=(1,1,1,1); а2=(3,3,-1,-1); а3=(-1,0,3,4)

Построение:

1)Пусть b1 = а1=(1,1,1).

2)Пусть b2=а2+к *b2, b1  b2.

Умножим обе части равенства на b1.

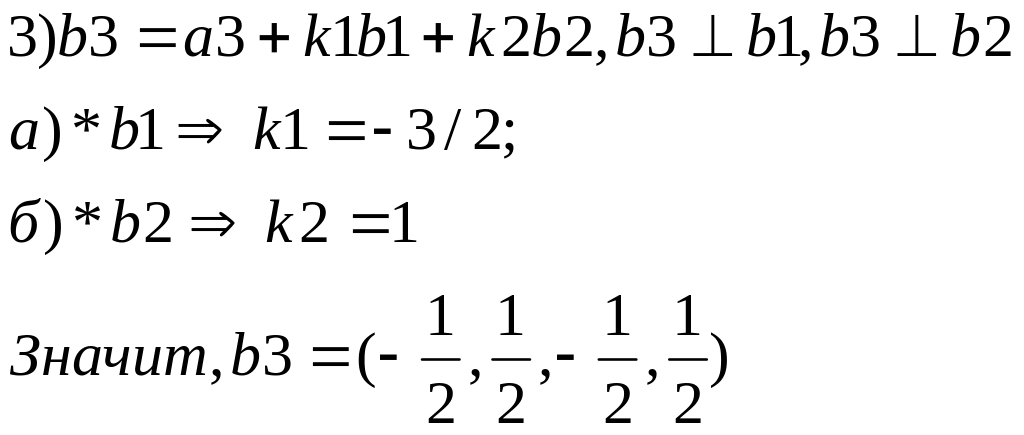
b1, b2, b3 – ортогональная система векторов