
- •1.Определение и примеры групп. Циклические группы
- •2. Определение и примеры колец. Типы колец
- •3. Определение и примеры полей. Характеристика поля
- •4. Изоморфизмы и гомоморфизмы групп, колец, полей.
- •5. Сравнения. Кольцо классов вычетов
- •6. Поле комплексных чисел
- •Алгебраическая запись
- •7. Кольцо многочленов от одной переменной над полем. Теория делимости.
- •8. Решение систем линейных уравнений с n неизвестными методом Гаусса
- •9. Решение систем линейных уравнений с n неизвестными по формулам Крамера
- •10. Матрица и её определитель. Свойства определителя n –го порядка
- •11. Обратная матрица. Способы нахождения обратной матрицы.
- •12. Ранг матрицы. Основные теоремы о ранге матрицы. Теорема Кронекера-Капелли. Общее решение систем алгебраических уравнений
- •13. Векторные пространства. Подпространства. Размерность и базис
- •14. Евклидово пространство. Процесс ортогонализации векторов
- •15. Линейные преобразования и их матрицы
- •16. Собственные векторы и собственные значения линейных операторов
- •17. Подгруппы. Смежные классы по подгруппе, фактор-группы.
- •18. Подкольца. Идеалы кольца, фактор-кольца. Кольца главных идеалов
- •19. Евклидовы и факториальные кольца
- •20. Факториальность кольца многочленов над факториальным кольцом
- •21. Многочлены от нескольких переменных, симметрические многочлены.
- •22. Алгебраическая замкнутость поля комплексных чисел.
- •Свойства
- •Свойства
- •24. Простые и конечные расширения числовых полей.
- •25. Неразрешимость некоторых классических задач на построение циркулем и линейкой.
6. Поле комплексных чисел
Опр1.
Алг-ское
расширение
поля
действительных
чисел
![]() с
помощью элемента
с
помощью элемента
![]() ,
являющегося корнем
мн-на
,
являющегося корнем
мн-на
![]() ,
называется полем
комплексных чисел.
Поле комплексных чисел обозначается
через
,
называется полем
комплексных чисел.
Поле комплексных чисел обозначается
через
![]()
Т-ма
1.(Осн-ая
т. алгебры.)
Поле комплексных чисел
алгебраически
замкнуто,
т.е. Опр1.
Поле
![]() называется
алгебраически
замкнутым,
если всякий многочлен
называется
алгебраически
замкнутым,
если всякий многочлен
![]() степени
не меньше 1 имеет корень
в
.
степени
не меньше 1 имеет корень
в
.
Пр 1. Поле комплексных чисел является алгебраически замкнутым.
Пр
2.
Поле
действительных чисел
не
является алгебраически замкнутым,
поскольку многочлен ![]() не
имеет корней в
.
не
имеет корней в
.
Плоскость комплексных чисел
Опр
2.
Полем
ком-х чисел
называется
множество всех упорядоченных пар
дейст-ых чисел (x,y).
При этом каждая такая пара z=(x,y)называется
комплексным
числом.
Таким образом, множество ком-ых чисел
можно интерпретировать как точки на
плоскости
![]() .
.
О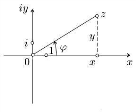 пределим
операцию сложения комплексных чисел
по правилу (x1,y1)+(x2,y2)=(x1+x2,y1+y2)
для всех (x1,y1),(x2,y2),
и определим операцию умножения:
(x1,y1)∙(x2,y2)=(x1x2-y1y2,
x1y2+x2y1)
для всех (x1,y1),(x2,y2)
пределим
операцию сложения комплексных чисел
по правилу (x1,y1)+(x2,y2)=(x1+x2,y1+y2)
для всех (x1,y1),(x2,y2),
и определим операцию умножения:
(x1,y1)∙(x2,y2)=(x1x2-y1y2,
x1y2+x2y1)
для всех (x1,y1),(x2,y2)
Пред1.
Множество
![]() является
полем.
является
полем.
Нулевым
элементом
в поле
является
пара (0,0),
а единичным
— пара (1,0).
Противоположный
элемент
для (x,y)—
это (-x,-y),
а обратным
для ненулевого (x,y)
является
![]() .
.
Алгебраическая запись
Опр 3.
Пусть i—
корень уравнения ![]() .
Полем
комплексных чисел
C
называется
множество объектов вида x+yi,
где x,y
.
Полем
комплексных чисел
C
называется
множество объектов вида x+yi,
где x,y
![]() ,
со следующими операциями сложения и
умножения:
,
со следующими операциями сложения и
умножения:
1.(x1+y1i)+(x2+y2i)=(x1+x2)+(y1+y2)i для всех
x1+y1i,
x2+y2i
![]() С.
С.
2. (x1+y1i)∙(x2+ y2i)=(x1x2-y1y2)+(x1y2+x2y1)i для всех x1+y1i, x2+y2i С.
Число i
называется мнимой единицей. Это опр.
легко получается из предыдущего, если
элементы (x,0)
обозначать через x,
а элемент (0,1) – через i.
Тогда произвольное комплексное число
(x,y)=(x,0)+(0,y)=(x,0)+(y,0)(0,1)
запишется в виде x+yi.
Т.к. (0,1)∙(0,1)=(0∙0 - 1∙1, 0∙1+1∙0)=(-1,0), то мнимая
единица i
является корнем ур-я ![]()

7. Кольцо многочленов от одной переменной над полем. Теория делимости.
Кольцо многочленов от одного переменного над полем является кольцом главных идеалов, т. е. любой его идеал может быть порожден одним элементом.
Более того, кольцо многочленов от одного переменного над полем является евклидовым кольцом.
Кольцо главных идеалов — кольцо, каждый идеал которого является главным. В случае некоммутативного кольца различают кольцо главных правых идеалов и кольцо главных левых идеалов.
Для кольца R идеалом называется подкольцо, замкнутое относительно умножения на элементы из R. При этом идеал называется левым (соответственно правым), если он замкнут относительно умножения слева (соответственно справа) на элементы из R. Идеал, являющийся одновременно левым и правым, называется двусторонним. Двусторонний идеал часто называется просто идеалом. В коммутативном случае все эти три понятия совпадают и всегда применяется термин идеал.
Более точно: Идеалом кольца R называется такое подкольцо I кольца R, что
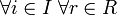 произведение
произведение
 (условие
на правые идеалы);
(условие
на правые идеалы);
произведение
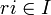 (условие
на левые идеалы).
(условие
на левые идеалы).
Аналогично для полугруппы её идеалом называется подполугруппа, для которой верно какое-нибудь из этих условий (или оба для двустороннего идеала), то же самое и для алгебры
Делимость
Многочлен, который можно представить в виде произведения многочленов низших степеней с коэффициентами из данного поля, называется приводимым (над данным полем), в противном случае — неприводимым. Неприводимые многочлены играют в кольце многочленов роль, сходную с ролью простых чисел в кольце целых чисел. Например, верна теорема: если произведение pq делится на неприводимый многочлен λ, то p или q делится на λ. Каждый многочлен, степени большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулевой степени).
Например, многочлен x4 + 2, неприводимый в поле рациональных чисел, разлагается на два множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.
Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).
Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен от n переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.

