9. Поверхности вращения

Пусть – плоская линия и – прямая, принадлежащая плоскости плоской линии.

Определение. Поверхность, получающуюся вращением плоской линии вокруг прямой, лежащей в плоскости плоской линии, называют поверхностью вращения.

Прямая, вокруг которой вращается плоская линия , называется осью вращения, а вращающаяся линия – первоначальным меридианом.

Пусть – секущая плоскость.

1) Если , то сечением служит окружность, проходящая через точку с центром на оси . Такие окружности называют параллелями.

2) Если : , то сечение – линия – меридиан. Любой меридиан поверхности вращения и первоначальный меридиан – равные линии.

Введем в рассмотрение прямоугольную декартову систему координат так, чтобы ось вращения совпала с осью .

Теорема 9.1. Пусть относительно прямоугольной декартовой системы координат на плоскости задан первоначальный меридиан поверхности вращения уравнениями

. (9.1)

Тогда уравнение поверхности , образованной вращением линии вокруг оси будет иметь вид

. (9.2)

► Пусть – первоначальный меридиан поверхности вращения ,

з аданный уравнениями , т.е. . И пусть – меридиан и – параллель: . Тогда . Так как , то . Точка – центр окружности-параллели . Так как точки и принадлежат одной и той же параллели , то , где – радиус окружности-параллели. Но .

Следовательно

Рис. 15. Поверхность вращения.

,

.

Тогда , и уравнение поверхности вращения имеет вид

. ◄

Рассмотрим некоторые примеры поверхностей вращения.

1) Пусть : – эллипс в плоскости .

Т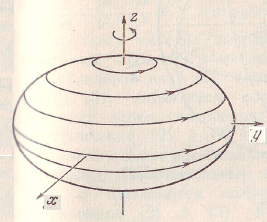 ак как показано, что и , то уравнение поверхности вращения имеет вид

или . (9.3)

Рис. 16. Эллипсоид вращения. (9.3) – эллипсоид вращения (Рис. 16).

В частности, если – окружность: , то, учитывая, что и , получаем уравнение поверхности вращения

или (9.4)

(9.4) – сфера с центром в начале координат радиуса (Рис. 17).

Рис. 17. Сфера.

2) Если : – гипербола в плоскости , то, учитывая, что и , уравнение поверхности вращения имеет вид

или

(9.5)

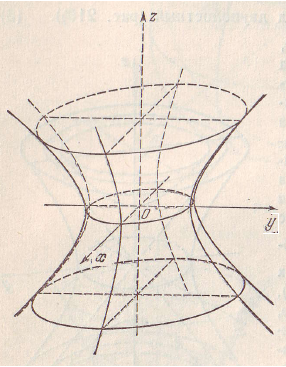
Рис. 18. Однополостный (9.5) – однополостный гиперболоид вращения.

гиперболоид вращения

3) Если : – гипербола в плоскости , то с учетом соотношений и , уравнение поверхности вращения имеет вид

или (9.6)

(9.6) – двуполостный гиперболоид вращения (Рис. 19).

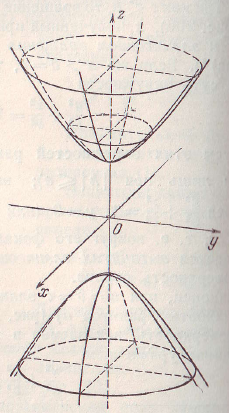
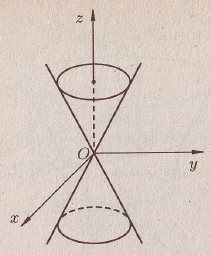
Рис. 19. Двуполостный Рис. 20. Прямой круговой конус

гиперболоид вращения.

4) Если : – прямая в плоскости . Тогда при и получаем уравнение поверхности вращения:

или (9.7)

(9.7) – прямой круговой конус (Рис. 20).

5) : – парабола в плоскости . Уравнение поверхности вращения имеет вид:

или (9.8)

(9.8) – параболоид вращения (Рис. 21).

6) : – прямая, параллельная оси . Учитывая, что и , получаем уравнение поверхности вращения:

или (9.9)

(9.9) – прямой круговой цилиндр (Рис.22).

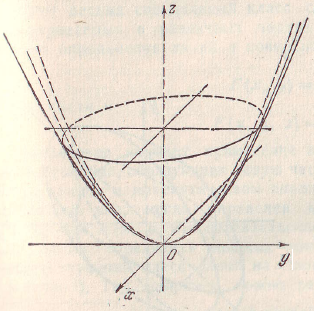
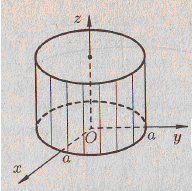
Рис.21. Параболоид вращения. Рис.22. Прямой круговой цилиндр

7) : – окружность в плоскости , не пересекающая ось . Тогда при и имеем:

(9.10)

(9.10) – тор (Рис. 23).

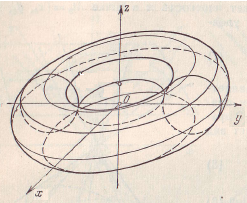
Рис. 23. Тор.