§7. Эллиптический параболоид

Определение. Множество точек пространства, координаты которых в некоторой прямоугольной декартовой системе координат удовлетворяют уравнению

, (7.1)

называют эллиптическим параболоидом.

Нетрудно показать, что ось является осью симметрии поверхности (7.1) (ее называют осью параболоида), а координатные плоскости и являются плоскостями симметрии (их называют главными плоскостями этой поверхности). Начало координат для эллиптического параболоида является точкой пересечения этой поверхности с ее осью и называется вершиной.

1) Сечения эллиптического параболоида плоскостями определяются уравнениями

(7.2)

а) При система (7.2) действительных решений не имеет. Следовательно, плоскость в этом случае не пересекает поверхность (7.1).

б) При система (7.2) имеет одно единственное решение – . Следовательно, плоскость является касательной к эллиптическому параболоиду (7.1) в его вершине.

в) При соотношения (7.2) равносильны системе

(7.3)

Уравнения (7.3) определяют эллипс, расположенный в плоскости . Его центр находится в точке , оси параллельны координатным осям и . Длины полуосей

и

изменяются от до при изменении от до соответственно.

2) Сечения эллиптического параболоида плоскостями определяются уравнениями

или (7.4)

Уравнения (7.4) определяют параболу, расположенную в плоскости . Ее вершина находится в точке , ось параллельна оси . При уравнения этой параболы принимают вид

(7.5)

3) Сечения поверхности (7.1) рассматриваются аналогично предыдущему случаю.

Приведенные рассуждения и сделанные при этом выводы позволяют получить представление о форме рассматриваемой поверхности (Рис. 14).

Рис. 14. Эллиптический параболоид

При уравнение поверхности (7.1) принимает вид

. (7.6)

Поверхность (7.6) изображена на рисунке 15.

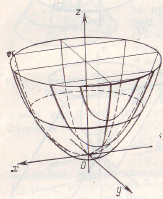
Рис. 15. Эллиптический параболоид вращения.

Ее называют параболоидом вращения, поскольку она может быть получена вращением параболы (7.5) вокруг оси . Любая плоскость, проходящая через ось , является плоскостью симметрии этой поверхности.

§8. Гиперболический параболоид

Определение. Множество точек пространства, координаты которых в некоторой прямоугольной декартовой системе координат удовлетворяют уравнению

, (8.1)

называют гиперболическим параболоидом.

Нетрудно показать, что ось является осью симметрии поверхности (8.1) (ее называют осью параболоида), а координатные плоскости и являются плоскостями симметрии (их называют главными плоскостями этой поверхности). Начало координат для гиперболического параболоида является точкой пересечения этой поверхности с ее осью и называется вершиной.

1) Сечения поверхности (8.1) плоскостями определяются уравнениями

(8.2)

а) Если , то соотношения (8.2) равносильны системе

(8.3)

Уравнения (8.3) определяют гиперболу, расположенную в плоскости . Ее центр находится в точке , действительная ось параллельна оси , мнимая – оси . Длины полуосей

и

изменяются от до при изменении от до соответственно.

б) Если , то соотношения (8.2) равносильны системе

(8.4)

Уравнения (8.4) определяют пару пересекающихся прямых

и ,

расположенных в плоскости и целиком лежащих на поверхности (8.1).

в) Если , то соотношения (8.2) равносильны системе

(8.5)

Уравнения (8.5) определяют гиперболу, расположенную в плоскости . Ее центр находится в точке , действительная ось параллельна оси , мнимая – оси . Длины полуосей

и

изменяются от до при изменении от до соответственно.

2) Сечения гиперболического параболоида плоскостями определяются уравнениями

или (8.6)

Уравнения (8.6) определяют параболу, расположенную в плоскости . Ее вершина находится в точке , ось параллельна оси , ветви направлены «вверх». При эта парабола расположена в плоскости , и ее уравнения имеют вид

(8.7)

3) Сечения гиперболического параболоида плоскостями определяются уравнениями

или (8.8)

Уравнения (8.6) определяют параболу, расположенную в плоскости . Ее вершина находится в точке , ось параллельна оси , ветви направлены «вниз». При эта парабола расположена в плоскости , и ее уравнения имеют вид

(8.9)

Приведенные рассуждения показывают, что гиперболический параболоид может быть получен движением параболы (8.7) по параболе (8.9) (при движении параболы (8.7) ее вершина перемещается по параболе (8.9)) или наоборот.

Приведенные рассуждения и сделанные при этом выводы позволяют получить представление о форме рассматриваемой поверхности.

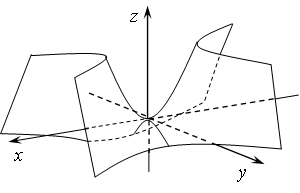
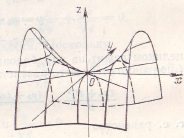
а) б)

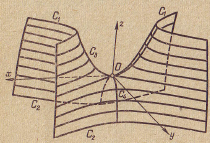
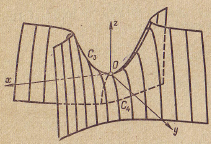
в) г)

Рис. 16. Гиперболический параболоид и его сечения.