Поверхности второго порядка

§1. Понятие алгебраической поверхности

Определение. Алгебраической поверхностью называют множество точек пространства, координаты которых относительно некоторой аффинной системы координат удовлетворяют уравнению

, (1.1)

где - целая рациональная функция (многочлен) степени от переменных .

Степень называют порядком поверхности.

Если уравнение (1.1) не является алгебраическим, то поверхность называют трансцендентной.

Если , то поверхность первого порядка – плоскость:

.

Если , то общее уравнение поверхности второго порядка относительно некоторой аффинной системы координат записывают в виде

(1.2)

причем очевидно, что .

Первые шесть слагаемых уравнения (1.2) называют его старшими членами, а их коэффициенты – старшими коэффициентами.

Для изучения поверхностей используют так называемый метод параллельных сечений.

Определение. Сечениями называют линии пересечения плоскостей с поверхностью.

Для определения формы поверхности по ее уравнению проводят ряд равноотстоящих друг от друга секущих плоскостей, как правило, частного расположения относительно системы координат (плоскостей, параллельных координатным плоскостям). В таком случае сечения называют линиями уровня изучаемой поверхности. Далее линии уровня проецируют на соответствующие координатные плоскости – получают так называемую карту. По форме и расположению линий на карте делают вывод о форме изучаемой поверхности.

§2. Цилиндрические поверхности

Пусть в некоторой аффинной системе координат заданы в плоскости некоторая линия уравнением

(2.1)

и некоторый ненулевой вектор :

Определение. Множество всевозможных прямых, параллельных вектору и пересекающих линию , называют цилиндрической поверхностью.

Линию называют при этом направляющей поверхности, а параллельные прямые – образующими.

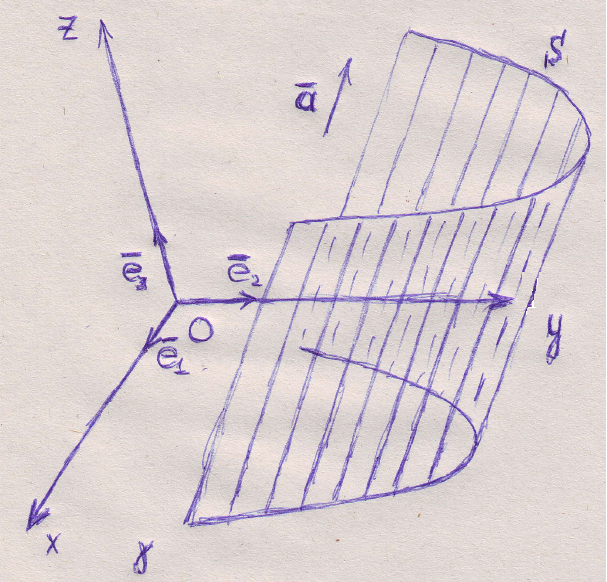
( - образующая) .

Очевидно, что векторы и коллинеарны. Следовательно, справедливы соотношения

.

Отсюда имеем .

Рис. 1. Цилиндрическая поверхность.

Подставляя эти равенства в (2.1), получаем соотношение

. (2.2)

Этому равенству удовлетворяют координаты тех и только тех точек, которые лежат на поверхности . Следовательно, (2.2) – уравнение цилиндрической поверхности.

Теорема 2.1. Если образующие цилиндрической поверхности параллельны оси , то уравнение такой поверхности по внешнему виду совпадает с уравнением ее направляющей.

► Действительно, если , то . Тогда соотношение (2.2) равносильно уравнению

, (2.3)

которое по внешнему виду полностью совпадает с уравнением (2.1) направляющей . ◄

В связи с этим можно дать другое определение цилиндрической поверхности.

Определение. Алгебраическую поверхность называют цилиндрической, если в некоторой аффинной системе координат ее можно задать алгебраическим уравнением, не содержащим одну из координат.

Теорема 2.2. Сечения цилиндрической поверхности параллельными плоскостями, пересекающими ее образующие, принадлежат одному и тому же аффинному классу кривых, к которому принадлежит ее направляющая.

Определение. Цилиндрическую поверхность называют поверхностью второго порядка, если ее направляющей является линия второго порядка.

◊ Для каждого из девяти видов линий второго порядка существует цилиндрическая поверхность с образующими, параллельными одной из координатных осей.

Примеры цилиндрических поверхностей второго порядка.

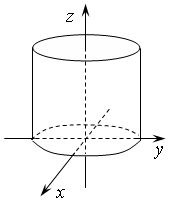
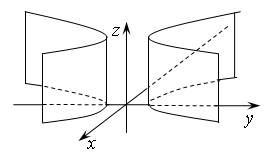
Рис. 2. Эллиптический цилиндр Рис. 3. Гиперболический цилиндр

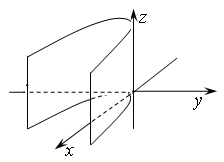
Рис. 4. Параболический цилиндр