Обратная функция

 

 

Если поменять ролями аргумент и функцию, то  x  станет функцией от  y. В этом случае говорят о новой функции, называемой обратной функцией.Предположим, мы имеем функцию:

 

v = u ² ,

 

где  u - аргумент, a  v - функция. Если поменять их ролями, то мы получим  u  как функцию  v :

Если обозначить аргумент в обеих функциях через  x , а функцию – через   y,  то мы имеем две функции:

каждая из которых является обратной по отношению к другой.

 

П р и м е р ы .  Эти функции являются обратными друг к другу:

                        

1)  sin x  и  Arcsin x,  так как, если  y = sin x,  то   x = Arcsin y;

2)  cos x  и  Arccos x,  так как, если  y = cos x,  то  x = Arccos y;

3)  tan x  и  Arctan x,  так как, если  y = tan x,  то   x = Arctan y;

4)  e^x  и  ln x,  так как, если  y = e^x ,  то  x = ln y.

Сложная функция

 

Рассмотрим функцию:

y = sin ² ( 2x ) .

 

Фактически эта запись означает следующую цепочку функциональных преобразований:

 

u = 2x  v = sin u  y = v²

 

что может быть записано в общем виде с помощью символов функциональных зависимостей:

 

u = f ₁ ( x )  v = f ₂ ( u )  y = f ₃ ( v ) ,

 

или короче:

y = f { v [ u ( x ) ] }.

 

Мы имеем здесь не одно правило соответствия для преобразования x в y, а три последовательных правила соответствия (т.е. функции ), используя которые мы получаем  y  как функцию от  x. В этом случае мы говорим, что  y – сложная функция от  x.

28

Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. Область значений функции - это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

7) Периодическость функции.

Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции. Также посмотрите материал про таблицу истинности, таблицу умножения, таблицу Менделеева, таблицу производных и таблицу интегралов.

29

	Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)
	Парабола - график функции квадратного трёхчлена у = ах2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0
	Гипербола - график функции  . При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а < 0).
	Экспонента (показательная функция по основанию е) у = еx. (Другое написание у = ехр(х)). Асимптота - ось абсцисс.
	Логарифмическая функция y = logax (a > 0)
	у = sinx. Синусоида - периодическая функция с периодом Т = 2π
	у = а•sin(ωx+φ) - функция гармонических колебаний. Обозначения: а - амплитуда, ω - частота (ω = 2π/Т), φ - фаза (сдвиг).
	Косинусоида у = cosx (графики у = sinx и у = cosx сдвинуты по оси х на  )
	Тангенсоида y = tgx. Точки разрыва при х =  (2k -1), где k = 0, ±1, ±2,.. Вертикальные асимптоты в этих точках.
	Гауссиана у = Аe-(ax2). Кривая "нормального" закона распределения ошибок, у которого ,  , σ 2 - дисперсия ошибки. Симметрия относительно оси у.
	у = secx - кривая "цепной линии", эту форму принимает абсолютно гибкая нить, подвешенная в параллельном поле тяжести. А полная функция периодична, и её асимптоты х =  (2k -1), как у функции y = tgx.
	Круг с центром в точке (xo, yo) радиуса r. (x-xo)2 + (y-yo)2 = r2
	Эллипсс центром в точке (xo, yo). Большая полуось а, малая b, эксцинтриситет ,

Преобразования есть в лекциях.

35

<="" a="" style="color: rgb(0, 0, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: 2; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: 2; word-spacing: 0px; -webkit-text-size-adjust: auto; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">

y = arctg x	y = arcctg x
функция обратная функции y = tg x, -  / 2 < x <   / 2	функция обратная функции y = ctg x, 0 < x <

	y = arctg x	y = arcctg x
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ:	R	R
ОБЛАСТЬ ЗНАЧЕНИЙ:		(0;  )
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ:	нечетная	ни четная, ни нечетная
НУЛИ:	y = 0 при x = 0	нулей нет
ПРОМЕЖУТКИ  ЗНАКОПОСТОЯНСТВА:	y > 0, при x   (0;  ]  y < 0, при x   (- ; 0)	y > 0 при x   R
ЭКСТРЕМУМЫ:	нет	нет
ПРОМЕЖУТКИ  МОНОТОННОСТИ:	возрастает при x   R	убывает при x   R

arctg x + arcctg x =  /2

36

Последовательность – функция, область определения которой – множество всех натуральных чисел (за исключением, быть может, конечного числа таких чисел).Множество значений такой функции – их называют членами последовательности – может состоять из элементов любой природы (чисел, точек, векторов, функций, случайных величин и т.д.). Тогда говорят соответственно о последовательности чисел (числовой последовательности), последовательности точек и т.д.

Если натуральному числу n соответствует член последовательности x_n, последовательность записывается в виде {x₁; x₂; …; x_n; …} или кратко {x_n}.

 Арифметическая прогрессия 

     Арифметическая прогрессия - числовая последовательность   определяемая условиями: 1)   2)   (d - разность арифметической прогрессии).

     Свойства арифметической прогрессии:

     Формула n-го члена: 

     Формулы суммы n первых членов:

     Геометрическая прогрессия 

     Геометрическая прогрессия - числовая последовательность   определяемая условиями: 1)   2)   n = 1, 2, ...(q - знаменатель геометрической прогрессии).

     Свойства геометрической прогрессии:

     Формула n-го члена: 

     Формулы суммы n первых членов  :

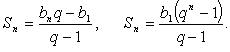
     Сумма бесконечной геометрической прогрессии:

Если каждому натуральному числу n поставлено в соответствие некоторое вещественное число    то говорят, что задана числовая последовательность   Кратко она обозначается символом      называют n-м членом последовательности. Совокупность этих чисел называют множеством значений последовательности.

Существует несколько способов задания числовых последовательностей.

1. Последовательность может быть задана при помощи формулы, позволяющей вычислить каждый ее член по номеру (например,   ).

2. Часто последовательность задается при помощи рекуррентной формулы, позволяющей определить каждый член последовательности по одному или нескольким предыдущим; при этом необходимо задание одного или нескольких первых членов последовательности. К таковым относятся арифметическая и геометрическаяпрогрессии или, например, последовательность Фибоначчи, задаваемая формулой 

   xn + 2 = xn + 1 + xn при n > 0

3. и условиями x₁ = 1, x₂ = 1.

4. Иногда последовательность задается описанием ее членов, например, последовательность, у которой x_n равен n-му знаку после запятой в десятичной записи числаπ = 3,14159265358979323..., задается следующим образом: x₁ = 1, x₂ = 4, x₃ = 1, x₄ = 5, x₅ = 9, x₆ = 2, x₇ = 6, x₈ = 5, x₉ = 3, x₁₀ = 5 и т. д.

Число a называется пределом последовательности {x_n}, если для каждого ε > 0 существует такой номер N_ε, что для всех n ≥ N_ε выполняется неравенство 

|xn – a| < ε,

т. е.   При этом пишут, что   или   при n → ∞. Кратко это определение можно записать так: 

Интервал (a – ε; a + ε) называют ε-окрестностью точки a.

Рисунок 1.1.1.1. ε-окрестность точки a.

Проще говоря, число a называется пределом последовательности {x_n}, если в любой ε-окрестности точки a лежат все члены последовательности {x_n}, за исключением, может быть, конечного их числа. Отсюда легко заметить, что изменение конечного числа членов последовательности не влияет ни на факт существования предела, ни на величину последнего.

Так, если   то   Действительно, выбрав для произвольного ε > 0   получаем  , так как   . Здесь существенно, что N_ε зависит от ε.

Для стабилизирующейся последовательности (т. е. последовательности {x_n} такой, что x_n = a при n ≥ n₀) в качестве N_εдля любого ε можно взять n₀.

Последовательность, у которой существует предел, называется сходящейся. Если никакое число не является пределом последовательности, то она называется расходящейся.

Можно показать, что числовая последовательность имеет только один предел.

Последовательность   называется возрастающей, если для любого   выполняется неравенство 

xn + 1 > xn.

Последовательность   называется убывающей, если для любого   выполняется неравенство 

xn + 1 < xn.

Если в этих определениях неравенство будет нестрогим, то последовательности будут называться соответственно неубывающей и невозрастающей.

Возрастающие и убывающие последовательности называют строго монотонными. Неубывающие и невозрастающие последовательности называют монотонными.

Теорема 1. Предел константы равен самой этой константе:

 c = с.

Говоря о пределе константы с, мы имеем в виду предел числовой последовательности

c, c, c, ..., c, ... ,

все члены которой равны одному и тому же числу с.

Теорема 2. Постоянный множитель можно выносить за знак предела:

 (kа_n) = k •    а_n.

Пример.   В § 130 было доказано, что

Поэтому

Теорема 3. Предел суммы двух переменных величин равен сумме пределов этих величин:

 (а_n + b_n) =   а_n +   b_n.

Пример.   В § 130 и 132 было доказано, что

  ,       

Поэтому

Данная теорема верна не только для двух, но и для произвольного фиксированного числа слагаемых. Например,

 (а_n + b_n + c_n + d_n) =   а_n +   b_n+   c_n +   d_n

Теорема 4. Предел   произведения двух переменных величин равен произведению пределов этих величин:

 (а_n • b_n) =   а_n •   b_n.

Пример.

И эта теорема верна не только для двух, но и для произвольного фиксированного числа сомножителей.  Например,

 (а_n • b_n • c_n • d_n) =   а_n •   b_n•   c_n •   d_n

Теорема 5. Предел дроби равен частному от деления предела числителя на предел знаменателя, если только предел знаменателя отличен от нуля:

Пример.    Пусть

в данном случае нельзя, поскольку   а_n = 0.

37

Теорема о промежуточной функции — одна из простейших теорем, изучаемых в рамках курса математического анализа.