Операции над множествами

 

Обозначение множеств и их элементов. Равенство множеств.

Подмножество ( включение ). Сумма ( объединение ) множеств.

Произведение ( пересечение ) множеств. Разность ( дополнение )

множеств. Симметричная разность множеств. Свойства

операций над множествами.

 

Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись  a   R  означает, что элемент  а  принадлежит множеству R , то есть  а  является элементом множества R . В противном случае, когда  а  не принадлежит множеству  R , пишут  a   R .  

 

Два множества А и В называются  равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества  А  является элементом множества  В  и наоборот, каждый элемент множества  В  является элементом множества  А .

 

Говорят, что множество А содержится в множестве В ( рис.1 ) или  множество А  является подмножеством множества  В ( в этом случае пишут А   В), если каждый элемент множества  А одновременно является элементом множества  В . Эта зависимость между множествами называется включением. Для любого множества  А имеют место включения:      А  и  А   А .

Сумма ( объединение ) множеств  А и В ( пишется  А   В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом,  е   А   В  тогда и только тогда, когда либо  е   А ,  либо  е   В .  

 

Произведение ( пересечение ) множеств  А и В ( пишется  А   В , рис.2 ) есть множество элементов, каждый из которых принадлежит и А , и В . Таким образом,  е   А   В  тогда и только тогда, когда   е   А  и  е   В .

Разность множеств А и В ( пишется  А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В.Это множество называется также дополнением множества В относительно множества А.

Симметричная разность множеств А и В ( пишется  А \ В  ) есть множество:

 

А \ В  = ( А – В )   ( В – А ).

 

 Свойства операций над множествами:

П р и м е р ы.  1. Множество детей является подмножеством всего населения.

 

                         2. Пересечением множества целых чисел с множеством поло-

                             жительных чисел является множество натуральных чисел.

 

 3. Объединением множества рациональных чисел с множест-

                             вом иррациональных чисел является множество действи-

                             тельных чисел.

 

                         4. Нуль является дополнением множества натуральных чисел

                             относительно множества неотрицательных целых чисел.

 

26

1. N - множество натуральных чисел возникло для подсчета количества чего-либо. 

N={1,2,...}. Бесконечное целое счетное множество. 

Z - множество целых чисел - бесконечное счетное дискретное множество. Z={0,-1,1,..}

Q - множество простых дробей вида p/q, в которых p, q - есть Z, причем q!=0. 

множество рациональных чисел составляют множество простых дробей, а также бесконечные периодические 

десятичные дроби. 

S - множество непереодических десятичных дробей, множество иррациональных чисел. 

R=Q U S - множество вещественных чисел. Множество действительных чисел R можно изобразить геометрически - 

точками числовой оси в виде значений некоторой переменной х, если у нас есть точка отсчета и некоторая единица 

масштаба. Между точками числовой оси х и вещественными числами R существует взаимоодназначное 

соответствие. Множество R - несчетное, то есть его элементы невозможно перенумеровать; мощность множества R 

больше мощности множества N. 

27

Среди всего многообразия явлений природы существуют такие, в которых взаимосвязь величин настолько тесна, что, зная значение одной из них, можно определить и значение другой.

Пусть задано числовое множество   Если каждому числу   поставлено в соответствие единственное число y , то говорят, что на множестве D задана числовая функция :  y  =  f  ( x ), 

Множество D называется областью определения функции и обозначается D  ( f  ( x )). Множество, состоящее из всех элементов f  ( x ), где   называется областью значений функции и обозначается E  ( f  ( x )).

Число x часто называют аргументом функции или независимой переменной, а число y – зависимой переменной или, собственно, функцией переменной x . Число     соответствующее значению   называют значением функции в точке   и обозначают   или 

Для того чтобы задать функцию f , нужно указать:

1) ее область определения D  ( f  ( x ));

2) указать правило f , по которому каждому значению   ставится в соответствие некоторое значение y  =  f  ( x ).

Запись       означает, что D  ( f  ( x )) = [–1; 2]. Если область определения не указана, то за область определения принимают множество всех значений аргумента, для которых данное выражение имеет смысл. Область определения иногда еще называют областью допустимых значений функции (ОДЗ). Для нахождения ОДЗ функции нужно проанализировать данное соответствие и установить встречающиеся запретные операции (деление на нуль, возведение в рациональную степень отрицательного числа, логарифмические операции над отрицательными числами и т. п.).

Функции f и g называются равными, если они имеют одну и ту же область определения D и для каждого   значения этих функций совпадают. В этом случае пишутf  ( x ) =  g  ( x ),   или f  =  g . Если же значения этих функций совпадают лишь на некотором множестве       и   то говорят, что функции равны на множестве     Так, например, функции f  = 1 и   равны на всем множестве   , а функции   и g  =  x равны на множестве    

Пусть функции f  ( x ) и g  ( x ) определены на одном и том же множестве D . Тогда функция, значения которой в каждой точке   равны f  ( x ) +  g  ( x ), называетсясуммой функций    f и g и обозначается f  +  g . Точно так же определяются разность    f  –  g , произведение    f  ·  g и частное    f  /  g двух функций (частное определено на множестве D , если на этом множестве g  ( x ) ≠ 0).

Пусть функции y  =  g  ( x ) и z  =  f  ( y ) определены на множествах D и E соответственно, причем множество значений функции f содержится в области определения функции g . Тогда функция, принимающая при каждом   значение f  ( g  ( x )), называется сложной функций или суперпозицией функций f и g и обозначается  Так, функция z  = sin ( x  – 1) является суперпозицией функций y  =  x  – 1 и z  = sin  y .  Важно отметить, что в общем случае суперпозиция   не совпадает с   ; так, в нашем примере  , а 

Функции могут задаваться различными способами. Самый распространенный из них – аналитический, когда числовая функция задается при помощи формулы. Вот некоторые примеры.

• Формулой S  ( r ) = π r ² задается функция зависимости площади круга от радиуса.

• Функция ºF (ºC) определяет перевод температуры из градусов Цельсия в градусы Фаренгейта: 

• Если деньги положены в банк под p процентов годовых, а сумма, положенная в банк изначально, равна     то через n лет в банке будет   – функция от количества лет, на которые положены средства    Эта формула называется формулой сложных процентов .

• При равномерном движении скорость тела является функцией времени: s  ( t ) =  v  ·  t .

• Функция x  ( t ) =  A  cos (ω t  + φ) задает гармонические колебания. Здесь A  – амплитуда колебаний, ω – круговая частота, φ – начальная фаза.

• Функция   называется формулой радиоактивного распада . Здесь   – начальное количество радиоактивного вещества, m  ( t ) – текущее, T – период полураспада.

Функция может быть задана различными формулами на разных промежутках. Так, формулы  f  ( x ) =    задают на множестве действительных чисел функцию f  ( x ) = | x |, называемою модулем , а формулы  f  ( x ) =    определяют функцию Дирихле . Иногда функция задается в виде таблицы численных значений. Наконец, функции могут задаваться при помощи графиков:

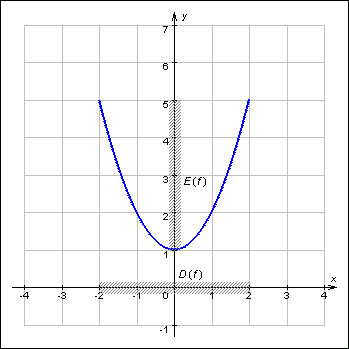 График 1.3.1.1.

График функции y  =  x ²  + 1 на D  = [–2; 2]. По числовым осям заштрихованы область определения и область значений функции.

Графиком функции y  =  f  ( x ) в выбранной системе координат называется множество всех точек ( x ;  y ), для которых выполняется равенство y  =  f  ( x ).

Для того, чтобы кривая на декартовой координатной плоскости была графиком функции, необходимо и достаточно, чтобы всякая прямая, параллельная оси ординат, либо не пересекалась с этой линией, либо пересекала ее в одной точке. Согласно этому определению окружность, например, не может быть графиком никакой функции, так как некоторым значениям x точек, принадлежащих этой кривой (например, абсциссе центра окружности), соответствуют два значения y .

Число a называется нулем функции   f  ( x ), если  f  ( a ) = 0.

График функции пересекает ось абсцисс в точках с абциссами, равными нулям функций.

Эскиз графика может быть построен выбором на оси OX нескольких значений аргументов x _i , построением точек ( x _i ,  f  ( x _i )) и соединением этих точек линиями. Если графиком функции является достаточно плавная кривая, то, соединяя полученные точки гладкой линией, мы получим эскиз искомого графика.

 Рисунок 1.3.1.1. Существуют функции, графики которых состоят из нескольких участков. К таковым, например, относится функция y  = sign ( x ). График функции y  = [ x ], где скобки означают взятие целой части числа, состоит из бесконечного количества отрезков. Наконец, ряд графиков функций не содержит ни одной «непрерывной» части. К таковым относится, например, числовая последовательность, которую можно определить как числовую функцию на множестве натуральных чисел 

Эскиз графика строится по нескольким точкам; линия эскиза графика на чертеже всегда конечной толщины (в то время как в математике линия графика считается бесконечно тонкой). Все это приводит к тому, что узнать значение функции по графику можно лишь приближенно. Тем не менее график является удобным средством для исследования функции и во многих случаях используется, чтобы визуально представить ход изменения функции.

Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.

Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

Функция может быть определена разными формулами на разных участках области своего задания.

Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.

Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Пример 1: функция E(x) — целая часть числа x. Вообще через E(x) = [x] обозначают наибольшее из целых чисел, которое не превышает x. Иными словами, если x = r + q, где r — целое число (может быть и отрицательным) и q принадлежит интервалу [0; 1), то [x] = r. Функция E(x) = [x] постоянна на промежутке [r; r+1) и на нем [x] = r.

Пример 2: функция y = {x} — дробная часть числа. Точнее y ={x} = x - [x], где [x] — целая часть числа x. Эта функция определена для всех x. Если x — произвольное число, то представив его в виде x = r + q ( r = [x]), где r — целое число и q лежит в интервале [0; 1), получим {x} = r + q - r=q

Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически.