Вопрос 20

общее уравнение второго порядка (11.15)определяет на плоскости (если не считать случаев вырождения и распадения) следующие кривые: окружность, эллипс, гиперболу, параболу.

Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

    (11.1)

Коэффициенты уравнения — действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка.

Вопрос 21

Уравнения прямой в пространстве - это уравнения двух пересекающихся плоскостей.

Напомним одну аксиому: если две плоскости в пространстве имеют общую точку, то они имеют общую прямую, на которой находятся все общие точки этих плоскостей. Таким образом, прямую линию в пространстве можно задать, указав две плоскости, пересекающиеся по этой прямой.

Итак, прямая в пространстве в прямоугольной системе координат Oxyz может быть задана системой из уравнений двух пересекающихся плоскостей .

Описание прямой линии уравнениями двух пересекающихся плоскостей отлично подходит при нахождении координат точки пересечения прямой и плоскости, а также при нахождении координат точки пересечения двух прямых в пространстве.

Следует отметить, что существуют различные способы задания прямой в пространстве, и на практике прямая чаще задается не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, лежащей на этой прямой. В этих случаях проще получить канонические и параметрические уравнения прямой в пространстве.

Параметрические уравнения прямой в пространстве.

Параметрические уравнения прямой в пространстве имеют вид , где x₁, y₁ и z₁ – координаты некоторой точки прямой, a_x, a_y и a_z (a_x, a_y и a_z одновременно не равны нулю) - соответствующие координаты направляющего вектора прямой, а - некоторый параметр, который может принимать любые действительные значения.

При любом значении параметра по параметрическим уравнениям прямой в пространстве мы можем вычислить тройку чисел , она будет соответствовать некоторой точке прямой (отсюда и название этого вида уравнений прямой).

Канонические уравнения прямой в пространстве.

Разрешив каждое из параметрических уравнений прямой вида относительно параметра , легко перейти к каноническим уравнениям прямой в пространстве вида .

Канонические уравнения прямой в пространстве определяют прямую, проходящую через точку , а направляющим вектором прямой является вектор . Следует отметить, что одно или два из чисел в канонических уравнениях прямой могут быть равны нулю (все три числа одновременно не могут быть равны нулю, так как направляющий вектор прямой не может быть нулевым). Тогда запись вида считается формальной (так как в знаменателях одной или двух дробей будут нули) и ее следует понимать как , где .

Если одно из чисел в канонических уравнениях прямой равно нулю, то прямая лежит в одной из координатных плоскостей, либо в плоскости ей параллельной. Если два из чисел равны нулю, то прямая либо совпадает с одной из координатных осей, либо параллельна ей. Например прямая, соответствующая каноническим уравнениям прямой в пространстве вида , лежит в плоскости z=-2, которая параллельна координатной плоскости Oxy, а координатная ось Oy определяется каноническими уравнениями .

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

• Общее уравнение (полное) плоскости

где и  — постоянные, причём и одновременно не равны нулю; в векторной форме:

где  — радиус-вектор точки(Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.) , вектор перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора :

Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При плоскость проходит через начало координат, при (или , ) П. параллельна оси (соответственно или ). При ( , или ) плоскость параллельна плоскости (соответственно или ).

• Уравнение плоскости в отрезках:

где , ,  — отрезки, отсекаемые плоскостью на осях и .

• Уравнение плоскости, проходящей через точку перпендикулярно вектору нормали :

в векторной форме:

• Уравнение плоскости, проходящей через три заданные точки 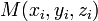, не лежащие на одной прямой:

(смешанное произведение векторов), иначе

• Нормальное (нормированное) уравнение плоскости

в векторной форме:

где - единичный вектор,  — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель

(знаки и противоположны).