9.Момент силы относительно произвольного центра. Момент силы относительно произвольной оси. Момент силы относительно произвольного центра.

Моментом силы называют количественную меру вращательного эффекта, вызываемого силой. Момент силы должен определять величину этого эффекта, плоскость поворота точки и направление поворота в этой плоскости.

(рис 23)

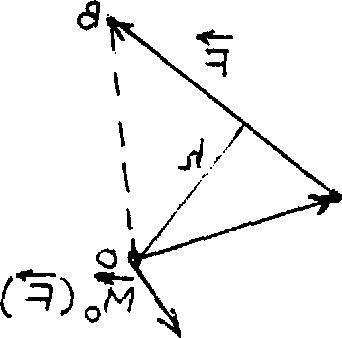
В еличина момента силы равна произведению модуля силы на ее плечо h (величину перпендикуляра, опущенного из заданного центра O на линию дей­ствия силы). Если начало вектора си­лы совпадает с точкой А, а конец – А с точкой В, то, очевидно, плоскость поворота совпадает с плоскостью треугольника OAB (рис. 23).

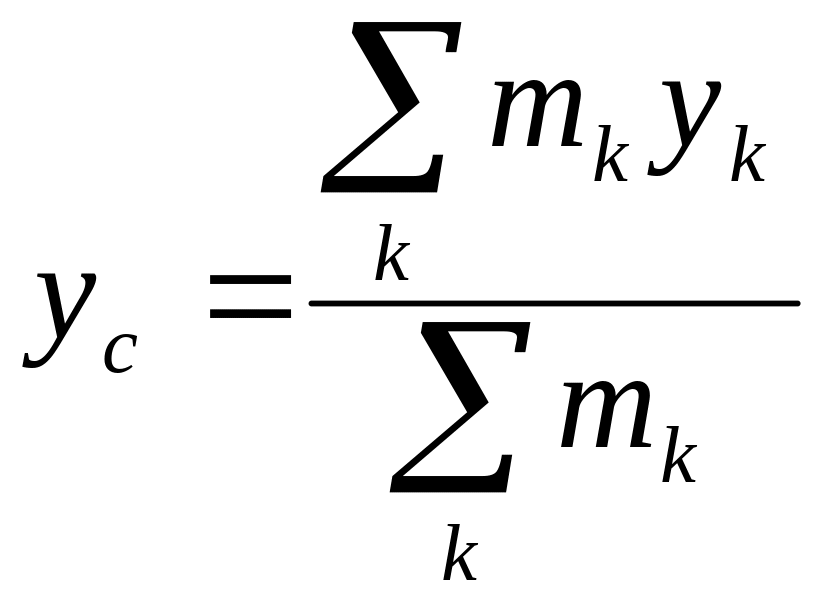
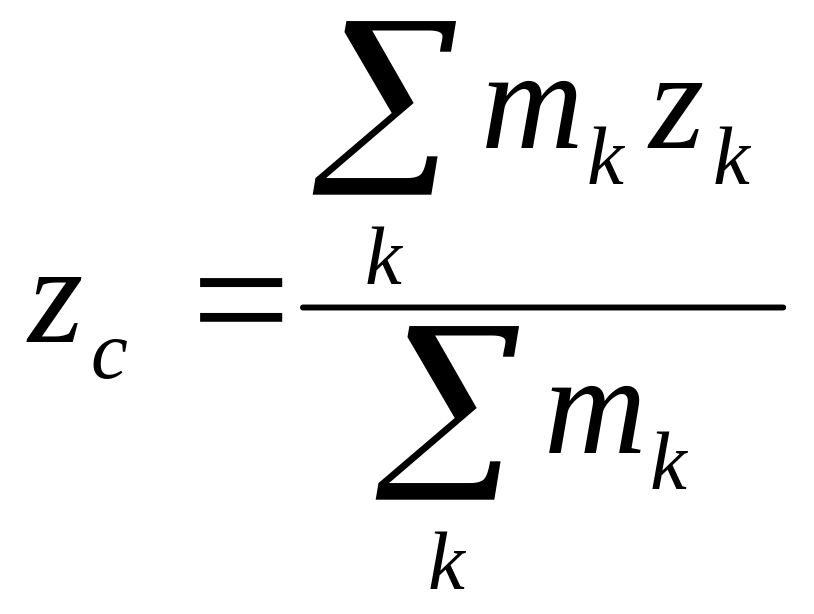
У словились вектор момента силы относительно центра M₀(F) проводить из этого центра O перпендикулярно плоскости поворота в ту сторону, откуда поворот виден происходящим против хода часо­вых стрелок. Модуль же вектора (длина вектора в выбранном масштабе) равен .

Очевидно, что такой вектор равен векторному произведению:

г де: r - радиус-вектор точки приложения силы, проведенный из заданного центра.

Момент силы относительно произвольной оси.

Моментом силы относительно оси называют величину, характеризующую вращательный эффект, вызываемый силой при вращении тела вокруг заданной оси.

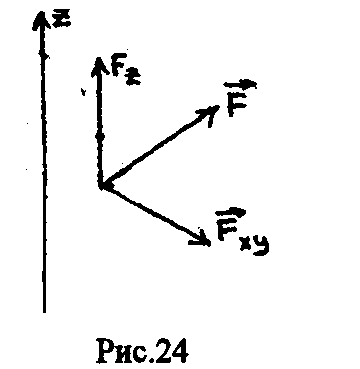
К телу А, способному вращаться вокруг оси z приложена сила F (рис. 24). Очевидно, что эффект вызываемый силой, определяется сум­мой эффектов, вызываемых ее проекциями F_z и F_xy, первая из кото­рых вращения тела вокруг оси z вызвать не может. Следовательно, момент силы относительно заданной оси определяется моментом ее про­екции на плоскость, перпендикуляр­ную оси, относительно точки Пересечения оси с плоскостью.

10. Основной закон динамики. Основной закон динамики. Уравнение моментов для тела движущего по окружности.

П усть точка движется по окружности радиуса с центром в т. О под действием силы F, составляющей угол a с каса­тельной а окружности (рис. 26).

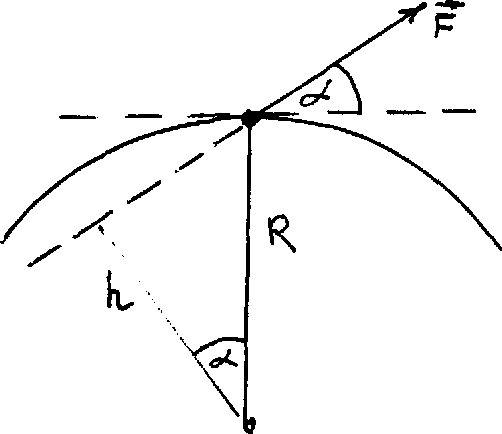(рис 26)

Второй закон динамики в проекциях на касательное направление имеет вид:

Учитывая, что и умно­жив обе части (61) на R получим:

из рисунка видно, что Rcosa=h (плечо силы относительно центра окружности). Учитывая также направление векторов углового ускорения и момента силы относительно центра окружности, получим:

С равним полученное выражение с основным законом динамики Ньютона в частной формулировке

З аметим, что в (63) и (64) физический смысл аналогичен, только речь идет о разных типах движения. Поэтому одинаков и физический смысл величин m и mR². Следовательно, величина mR² определяет инертные свойства тела при вращатель­ном движении. Эта величина I=mR² называется моментом инер­ции тела (точки). С учетом сказанного основной закон динамики для вращательного движения записывают в виде: