7 Сила. Сложение сил и разложение силы на составляющие. Проекции силы на плоскость и ось.

Изменение состояния тела происходит в результате взаимодей­ствий, которые приводят к изменению, как внутреннего состояния тел, так и состояния их движения. Количественной мерой взаимо­действий, приводящих к изменению состояний тел, является сила.

Сила - векторная величина, она характеризуется следующими элементами: величиной, направлением в пространстве и точкой при­ложения силы.

Линия, вдоль которой направлена сила, называется линией действия силы.

Совокупность сил, приложенных к телу, называют системой сил.

Если под действием системы сил, приложенных к телу, оно может пребывать в состоянии покоя, система называется уравновешенной

Если одну систему сил, приложенных к телу, можно заменить другой, не изменяя его состояние, системы называются эквивалентными.

Сила, эквивалентная системе сил, называется равнодействующей этой системы.

Сила, равная по величине равнодействующей и противоположно ей направленная, называется уравновешивающей.

Силы взаимодействия между телами одной и той же системы называются внутренними.

Силы взаимодействия с телами, не входящими в состав данной системы называются внешними.

Силы, приложенные в одной точке тела, называются сосредото­ченными.

Силы, приложенные ко всем точкам поверхности или объема тела, называются распределенными.

С ложение сил - задача нахождения равнодействующей для заданной системы сил. Находить равнодействующую можно аналитически и геометрически. В прос­том случае системы двух сил (рис. 18) можно аналитически выразить величину равнодействующей силы:

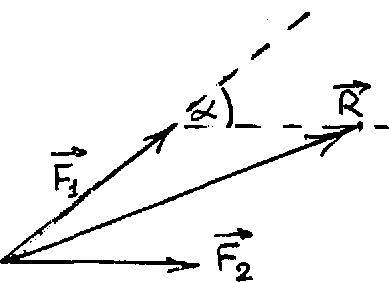где  - угол между направлениями сил системы.

является частным случаем правила силового многоугольника, по которому описанная операция проводится последовательно для всех сил системы, независимо от их ориентировки в пространстве. На­чало вектора равнодействующей совпадает с точкой приложения первой (по построению) силы системы, а конец - с концом вектора последней.

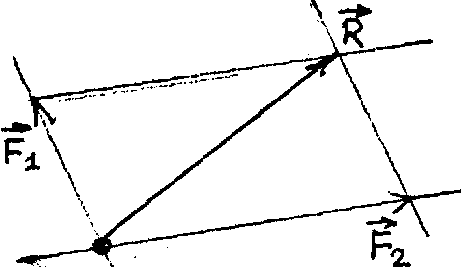Разложением сил на составляющие называют задачу нахождения системы сил, для которой данная сила является равнодействующей. Например, для искомой системы двух сил задают­ся направления линий действия сил системы (рис.20). Через начало и ко­нец вектора заданной силы проводят прямые, параллельные указанным направлениям. Искомые силы системы определяются сторонами полученного параллелограмма .

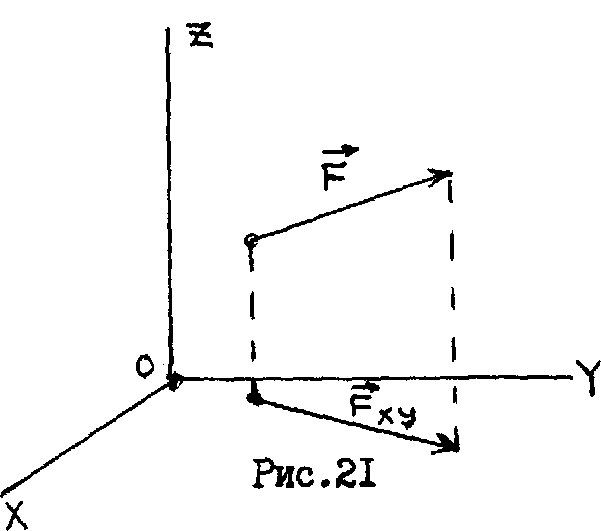
Проекцией силы на плоскость называют вектор F_xy, заключенный между проекциями начала и конца вектора силы на заданную плоскость (рис. 21).

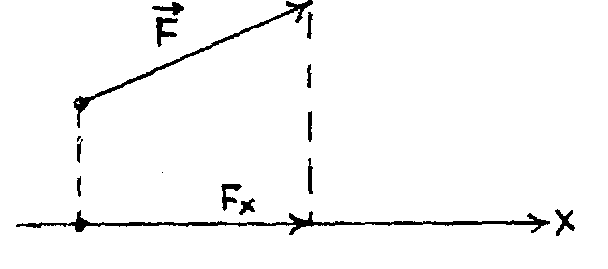
Аналогично - проекцией силы на ось называют отрезок, заключенный между проекциями начала и конца вектора силы на заданную ось (рис. 22).

В отличие от проекции на плоскость, проекция силы на ось является скалярной величиной.

8. Статическое и динамическое проявление сил. Законы Ньютона. Принцип независимости действия сил.

Статическое и динамическое проявление сил.

В процессе взаимодействия (в результате действия сил) тела изменяют свое внутреннее состояние и (или) состояние движения. В соответствии с этим рассматривают статическое проявление сил (приводящее к изменению внутреннего состояния тел) и динамическое (приводящее к изменению состояния движения). Например, при скольжении тела по наклонной плоскости сила его тяжести проявля­ется двояким образом: сообщая телу ускорение (динамически) и деформируя его в результате взаимодействия с наклонной плоскостью (статически). Поэтому в самом общем смысле все способы измерения сил можно разделить на два класса - статические и динамические. Пример: пружинный динамометр и акселерометр.

1-й ЗАКОН НЬЮТОНА (ЗАКОН ИНЕРЦИИ). Существуют такие системы отсчета, в которых тело, предоставленное самому себе, может находиться в состоянии покоя или равно­мерного и прямолинейного движения, пока и поскольку действие внешних сил не вынудят его изменить это состояние.

Способность тел сохранять состояние покоя или равномерного и прямолинейного движения, препятствуя внешним воздействиям, на­зывается инертностью. Это – внутреннее свойство, присущее всем телам, независимо от их природы и состояния. Причины же, вызыва­ющие изменения состояния тела, всегда внешние - это силы.

Количественной мерой инертности тел является их масса.

2-й ЗАКОН НЬЮТОНА (ОСНОВНОЙ ЗАКОН ДИНАМИКИ).

Как и все законы динамики основной закон получен опытным путем. В частном случае, когда масса тела в процессе взаимодей­ствий не изменяется, основной закон динамики формулируется в форме: ускорение, получаемое телом в результате действия на него системы сил, прямо пропорционально

равнодействующей приложенной системы сил, обратно пропорционально массе тел и направлено вдоль линии действия равнодействующей.

Математическая формулировка частной формы основного закона динамики имеет вид:

где: F - равнодействующая приложенной системы сил.

Более общей является следующая формулировка основного закона:

Изменение импульса тела пропорционально импульсу равнодействующей приложенной системы сил и направлено вдоль линии дей­ствия равнодействующей.

Под импульсом силы понимают произведение силы на время ее действия. Математическая формулировка общей формы основного за­кона динамики имеет вид:

3-й ЗАКОН ДИНАМИКИ (ЗАКОН ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ).

Существует две равноправные формулировки 3-го закона:

1. Действию всегда есть равное и противоположно направленное противодействие

2. Тела действуют друг на друга с силами, равными по вели­чине и противоположно направленными.

Эти формулировки получены в результате обобщения экспери­ментальных фактов, которые свидетельствуют о том, что тела взаимодействуют всегда попарно, т.е. на изолированное тело силы не действуют.

С 3-м законом динамики тесно связан закон сохранения импуль­са. Действительно, если на два тела действуют только силы взаимодействия между ними, то, по 3-му закону динамики, эти силы рав­ны по величине и противоположно направлены. Следовательно, по основному закону, одинаковы и противоположно направлены изменения импульсов тел, а общий импульс системы тел не изменяется.

ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ.

Если на тело действует несколько сил, то каждая из них сообщает телу ускорение, определяемое основным законом динамики, так, как если бы других сил не было.

Н апример, произвольно направленную и в пространстве силу F можно представить в виде суммы ее составляющих (компонентов):

где e_x, e_y, e_z - орты прямоугольной системы координат OXYz.

Второй закон динамики в этом случае имеет вид:

откуда:

Т. о., в приведенном рассуждении учтен принцип независимости действия сил.