4 Вращательное движение твердого тела.

Вращательным называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными в пространстве. Прямая, проходящая через не­подвижные точки тела, называются осью вращения. При вращательном движении все точки тела движутся в параллельных плоскостях, описывая концентрические окружности, центры которых лежат на оси вра­щения.

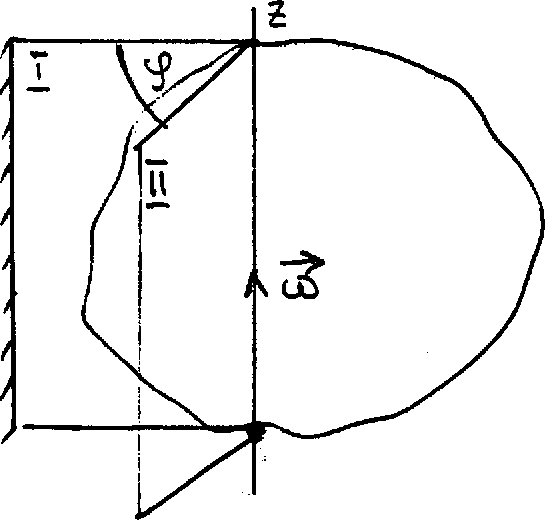
Пусть тело вращается вокруг неподвижной оси Z . Для определения положения этого тела в пространстве через ось вращения проведем две плоскости: 1 - неподвижную и 2 - связанную с телом и вращающуюся вместе с ним. Положение тела задается углом  между плоскостями (угловой координатой). Изменение угловой координаты задает угловое перемещение . Кинематический закон движения тела задан, если известна угловая координата в любой момент времени: = (t).

Быстрота вращения определяется угловой скоростью.

С редней угловой скоростью называют величину:

а мгновенной:

д ля определения  как вектора необходимо угол поворота (угловое перемещение) также определять как вектор. Вектором угло­вого перемещения называют вектор, направленный вдоль оси вращения в ту сторону, откуда вращение тела видно происходящим против хо­да часовых стрелок. По такому определению вектор угловой скорос­ти равен:

5 Движение отдельных точек вращающегося твердого тела.

Х отя все точки вращающегося тела имеют одинаковые и кинематические

характеристики их движения ( и ) различаются. Предположим, что произвольная точка вращающегося тела находится на расстоянии г от оси вращения.

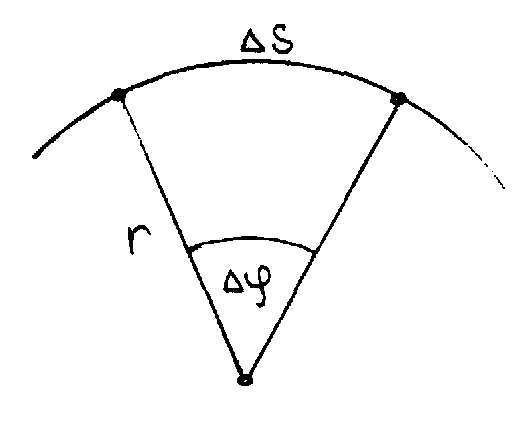
За промежуток времени t проходит по своей траектории путь S . Средняя скорость точки при этом равна:

а мгновенная:

С учетом направлений векторов угловой и линейной скорости, а также радиус-вектора рассматриваемой точки, получим:

У скорение отдельных точек вращающегося твердого тела удобно определять по отдельным его составляющим a_t, a_n:

Полное ускорение точки равно

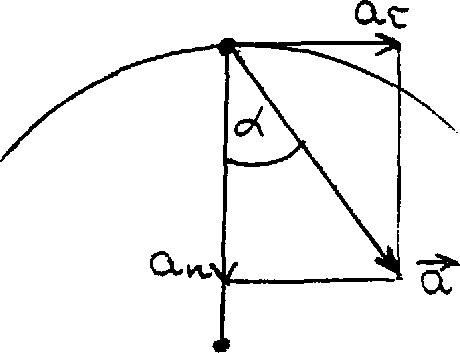
К ак видно из приведенных соотношений, полное ускорение и отдельные его составляющие зависят от расстояния r до оси вращения. Направление вектора ускорения при таком представлении определяется уг­лом отклонения  вектора ускорения от радиуса вращения .

Из рисунка видно, что

Таким образом, угол отклонения вектора полного ускорения от радиуса вращения одинаков для всех точек тела.

6 Плоское движение твердого тела

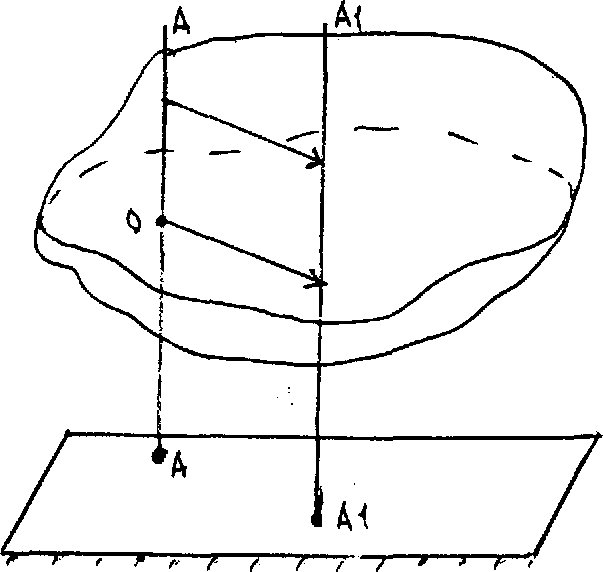
Плоским называют такое движение тела, при котором все его точки дви­жутся в плоскостях, параллельных за­данной неподвижной. Проведем связанную с телом нормаль АА к заданной неподвижной плоскости и, как показа­но на рис. 13, двигаясь вместе с те­лом, через промежуток времени dt нормаль занимает положение A₁А₁. Очевидно, что все точки тела, ле­жащие на этой нормали, движутся оди­наково, в частности, так же, как и точка O пересечения нормали с сечением тела плоскостью, параллель­ной заданной неподвижной. То же можно сказать о точках тела, ле­жащих на любой другой нормали. Поэтому для изучения плоского дви­жения тела достаточно рассмотреть движение его сечения плоскостью, параллельной заданной, т.е. решить задачу кинематики в плоской системе координат.

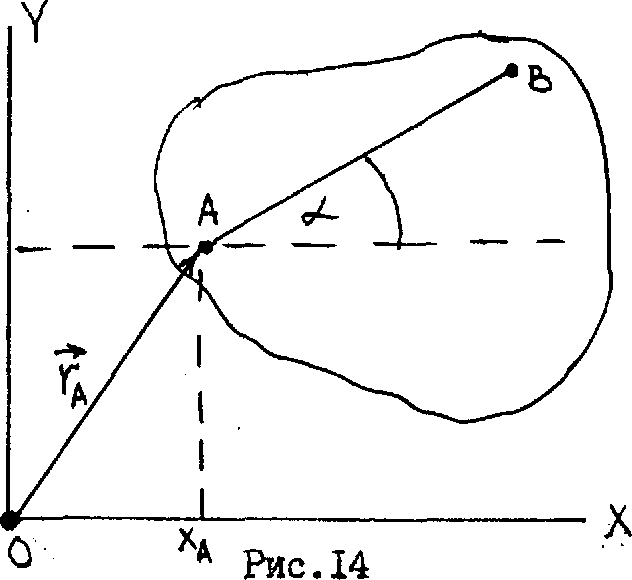
Для определения положения се­чения в пространстве в любой момент времени необходимо прежде всего задать положение произволь­ной точки А (полюса) этого сечения векторным или координатным способом. Кроме того, необходимо провести в сечении произвольную прямую АВ и указать угол a (альфа), кото­рый она образует с одной из осей координат (рис. 14). Движение сечения считается

заданным, если для любого момента времени известны зависимости:

и ли