38. Сообщающиеся сосуды, заполненные однородной жидкостью

Свободные поверхности в левом и правом коленах находятся на уровнях Z₁ и Z₂, а давление на этих поверхностях равно атмосферному Р_a. Сравним свободные поверхности с общей для обоих сосудов частью, уровнем Z₀, на котором давление равно P₀, как показано на рисунке

Откуда:

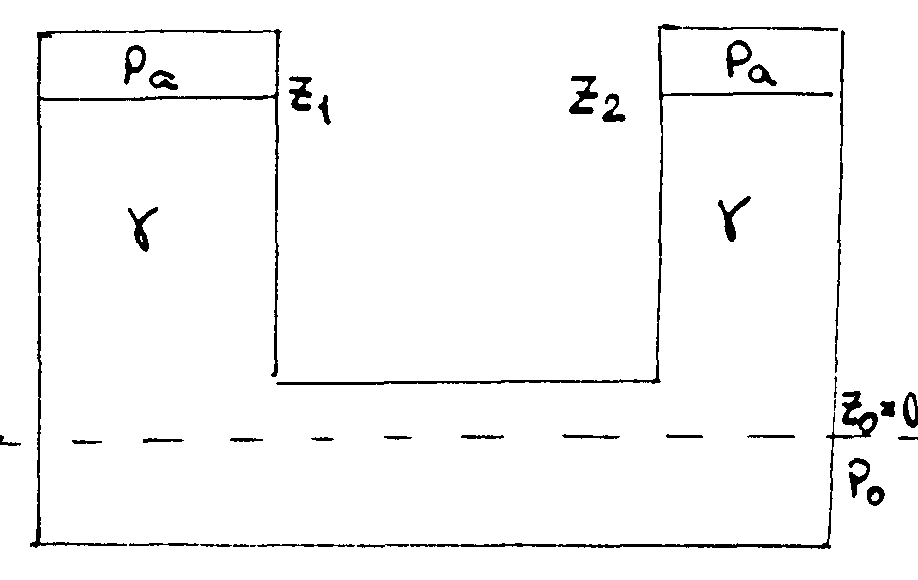
Следовательно, свободные поверхности устанавливаются на одном уровне.

39.Закон Архимеда.

Тело погружено в жидкость

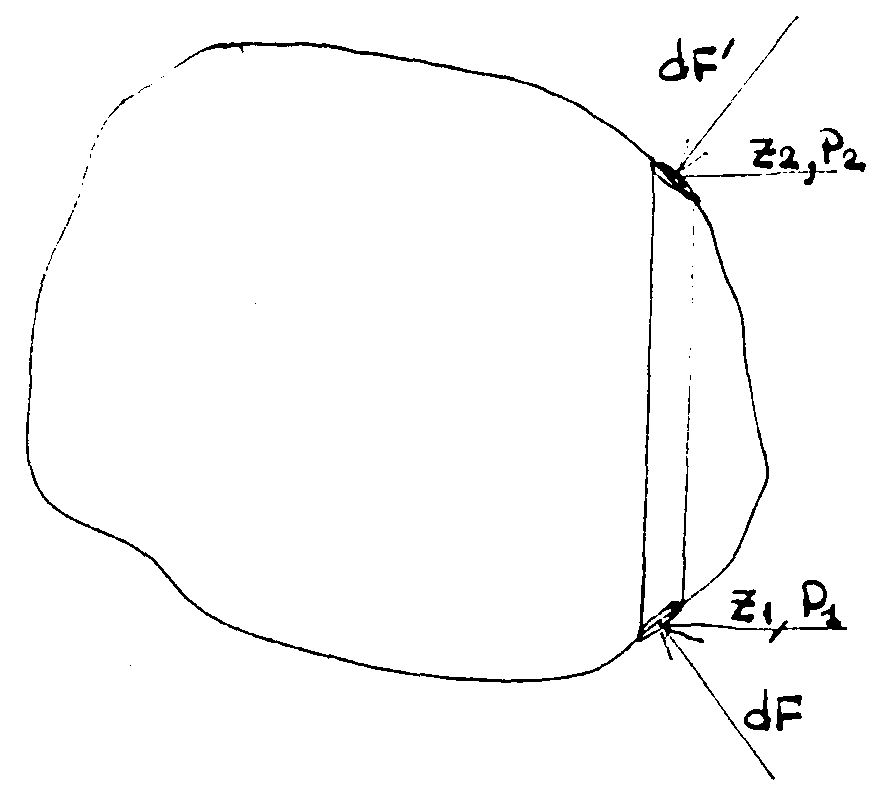
На его поверхность со стороны жидкости действуют силы давления, выделим в теле объем малого сечения, ось которого вертикальна. На верхнюю и ниж­нюю грани этого объема действу­ют силы давления

Равнодействующая сил давле­ния в проекции на вертикальную ось равна:

где: dS - проекция dS₁ (или dS₂) на горизонтальную плоскость. Разность давлений по закону Паскаля равна

где: dZ - разность уровней центров граней выделенного объема. Тогда равнодействующая сил давления равна

где dV - величина выделенного объема.

Вертикальная проекция сил давления, действующих на всю смоченную поверхность тела, может быть получена путем интегри­рования предыдущего выражения:

т.е. сила, действующая со стороны жидкости на погруженное в нее тело по величине равна весу жидкости, вытесненной телом.

Формулировка закона: на тело, погруженное в жидкость действует выталкивающая сила, равная весу жидкости в объеме, вытесненном телом , и приложенная в той точке смоченной поверхности тела, в которой вертикаль, проведенная через центр масс вытесненной жидкости, пересекает эту поверхность.

Существенным в формулировке закона Архимеда является правильное указание точки приложения выталкивающей силы. Действительно, поскольку сила Архимеда обусловлена действием рас­пределенных по поверхности сил давления со стороны жидкости, то и равнодействующая сил давления должна быть приложена к смоченной поверхности тела (но не к центру масс вытесненной жидкости, как это часто утверждается). Кроме того, наличие в плавающем теле деформаций можно объяснить только при таком рассмотрении силы Архимеда.

40. Механика движущихся жидкостей. Расход жидкости. Уравнение неразрывности струи жидкости.

При изучении движения жидкостей и газов применяются различ­ные способы описания движения. Наиболее часто используется метод, предложенный Эйлером. Но Эйлеру в области пространства, занятой движущейся жидкостью, выделяется точка, в которой определяются параметры движения различных жидких частиц, проходящих через эту точку в различные моменты времени.

Основной задачей механики движущейся жидкости является нахождение распределений скорости, плотности и давления по потоку жидкости:

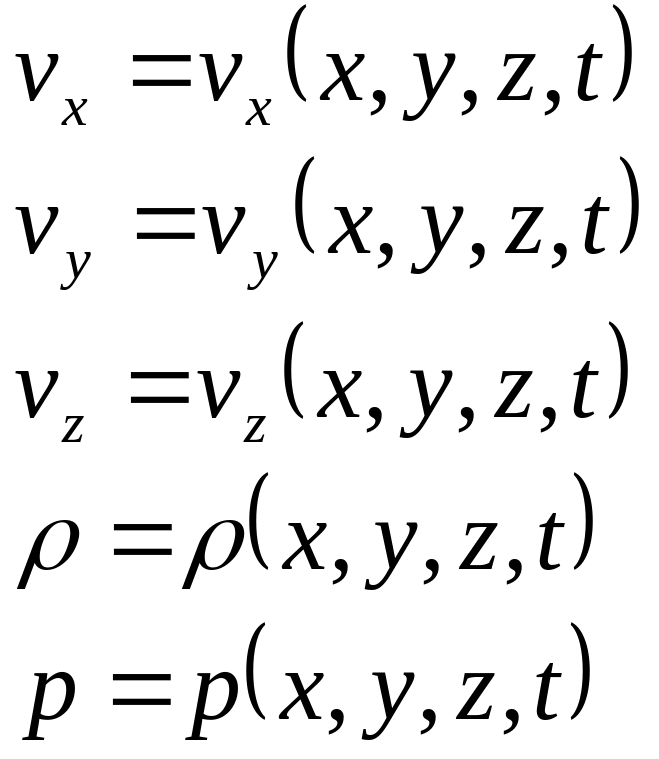
Для установившегося потока, когда параметры потока в фиксированной точке его не изменяются с течением времени, задача сводится к нахождению распределений:

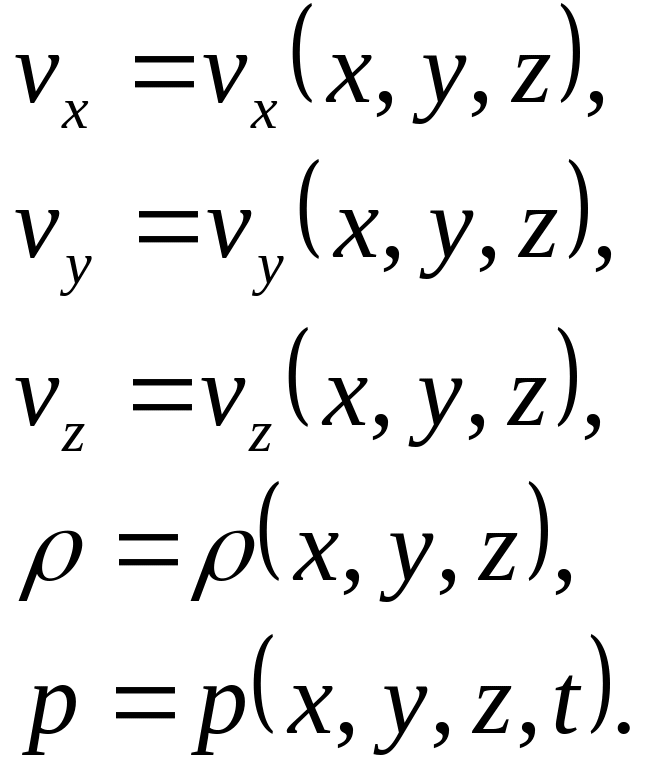
Ещё более упрощается задача для идеальной жидкости. В случае установившегося потока идеальной жидкости необходимо найти распределения:

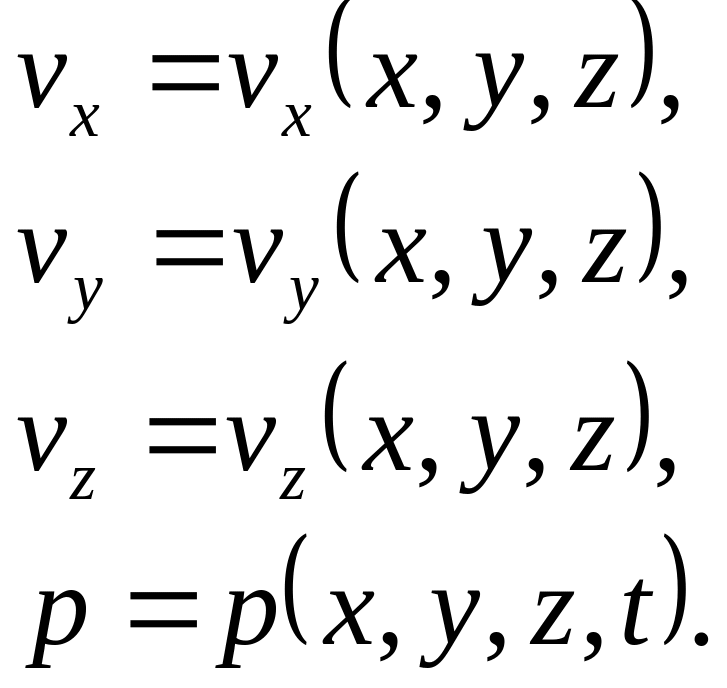
ОПРЕДЕЛЕНИЯ

1.Линией тока называют кривую, в каждой точке которой касатель­ные к ней совпадают по направлению с вектором скорости в данный момент времени.

2.Поверхностью тока называют поверхность, образованную линиями в тока.

3.Поверхность тока, проходящую через замкнутый контур, называют трубкой тока.

4.Часть потока жидкости, ограниченную трубкой тока, называют струёй жидкости.

Пpи установившемся потоке жидкость внутри трубки тока а движется как в трубке с твердыми стенками.

УРАВНЕНИЕ НЕРАЗРЫВНОСТИ СТРУИ ЖИДКОСТИ

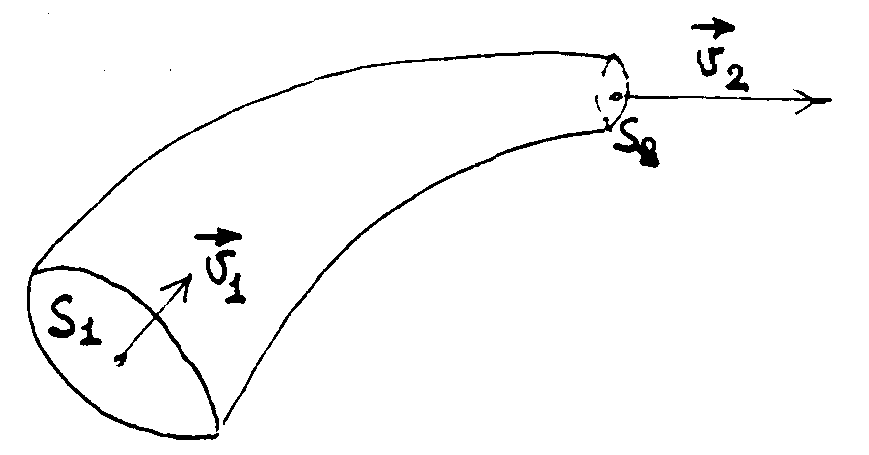
Оделим участок струи жидкости. Через левое сечение площади S₁ в участок трубки тока в единицу времени втекает жидкость со скоростью v₁ , принимаемой одинаковой по сечению. Массовый расход жидкости в этом сечении равен:

Аналогично массовый расход для правого сечения равен:

Для того, чтобы в выделенном участке трубки тока не происходило накопление жидкости или, наоборот, уменьшение массы, массовые расходы в левом и правом сечениях должны быть равны. Такой вывод можно сделать для любого другого сечения, т.е.:

Это и есть уравнение неразрывности струн жидкости. В случае несжимаемой жидкости: