17. Преобразования Лоренца. Интервал. Инвариантность интервала.

Преобразования Лоренца дают связь между пространственными и временными координатами событий в двух инициальных системах отсчета, находящихся в относительном движении.

Учитывая, что поперечные размеры тел одинаковы, получаем:

z'=z (166)

х'=x (167)

Для сравнения координат у обратимся к предыдущему примеру:

С другой стороны, это соотношение можно представить в виде:

Соотношения (166,167,168,170) называют преобразованиями Лоренца.

Интервал. Инвариантность интервала.

И нтервалом S между двумя событиями называют величину, квадрат которой равен:

где x_i,y_i,z_i,t_i - пространственные и временные координаты событий.

И спользуя преобразования Лоренца, запишем интервал в подвижной системе отсчета:

Таким образом, интервал является инвариантом:

S ^/2=S ² (171)

В зависимости от соотношения между временной cΔt и -

пространственной частями интервала различают:

1.Времениподобные интервалы (cΔt > Δl).

2.Пространственноподобные интервалы (cΔt <s Δl).

3. Светоподобные интервалы (сΔt = Δl).

17. Релятивистская масса, релятивистский импульс. Релятивистское уравнение движения.

И з факта предельности скорости света следует, что тела могут двигаться только со скоростями, меньшими скорости света. Если на тело действует постоянная сила, то его ускорение пропорционально силе лишь при малых скоростях. С ростом скорости при неизменной силе ускорение начинает уменьшаться, что можно объяснить только возрастанием массы тела с ростом скорости.

Масса тела, движущегося со скоростью  , равна:

Г де , - масса тела в системе, связанной с ним, так называемая "масса покоя".

Соответственно, импульс тела определяется выражением:

Релятивистское уравнение движения.

Р елятивистское уравнение движения по внешнему виду совпадает с записью основного закона динамики Ньютона в общей формулировке:

Р елятивистское уравнение динамики удовлетворяет преобразованиям Лоренца и, следовательно, общефизическому принципу относительности. Важно отметить, что в отличие от классического закона динамики в релятивистском случае сила и ускорение могут не совпадать по направлению:

Лишь в двух случаях, когда сила нормальна к вектору скорости или сонаправлена с ним, ускорение и сила по направление совпадают.

17. Неинерциальные системы отсчёта. Силы инерции. Силы инерции во вращающихся системах отсчета. Силы инерции Кориолиса.

Силы инерции

Как уже отмечалось, существуют такие системы отсчета, в которых ускорение тел вызывается не только действием сил, но и самим движением системы отсчета.

Рассмотрим поведение свободного тела, находящегося в покое относительно неподвижной системы. В этой системе выполняются законы Ньютона: равнодействующая приложенных к телу сил равна нулю и тело, как следствие, находится в покое. Если же другая система отсчета движется относительно первой с ускорением a, то в подвижной системе тело получает ускорение - а, равное по величине ускорению системы и противоположно ему направленное. Следовательно, в подвижной системе законы Ньютона не выполняются: равнодействующая приложенных сил равна нулю, а тело приобретает ускорение.

Ч тобы и в таких системах выполнялись законы Ньютона, приходится вводить дополнительные фиктивные силы, называемые силами инерции. В рассмотренном примере в подвижной системе вводится сила инерции:

объясняющая появление ускорения тепа в подвижной системе отсчета. Т.е. сила инерции равна произведению массы тела на ускорение системы и противоположно ему направлена.

Если связать систему отсчета с ускоренно движущимся телом, то геометрическая сумма всех сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера).

Силы инерции во вращающихся системах отсчета.

В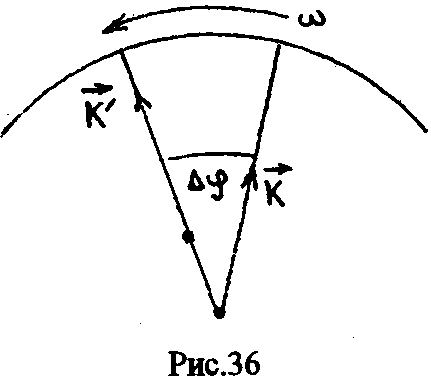 о вращающихся системах отсчета возникающие силы инерции зависят не только от движения системы, но и от характера движения тела относительно нее. Положим, что тело покоится во вращающейся системе и вращается вместе с ней. Для неподвижного наблюдателя тело движется по окружности, следовательно, на него действует реальная центростремительная сила. Во вращающейся системе тело покоится, хотя на него и действует указанная сила. Для выполнения законов динамики приходится ввести фиктивную силу, уравновешивающую центростремительную.Такую силу называют центробежной силой инерции.

При движении тела относительно вращающейся системы приходится вводить дополнительные силы инерции.

Силы инерции Кориолиса.

П усть система вращается равномерно с угловой скоростью ω. Вдоль радиуса системы равномерно со скоростью v движется тело (рис. 36).

Абсолютный импульс тела определяется относительным и переносным движением

Со временем будут изменяться обе составляющие абсолютного импульса. Рассмотрим сначала изменение относительного импульса.

П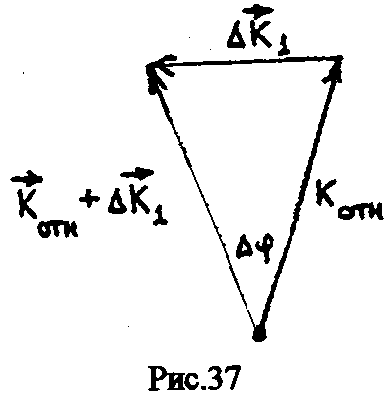 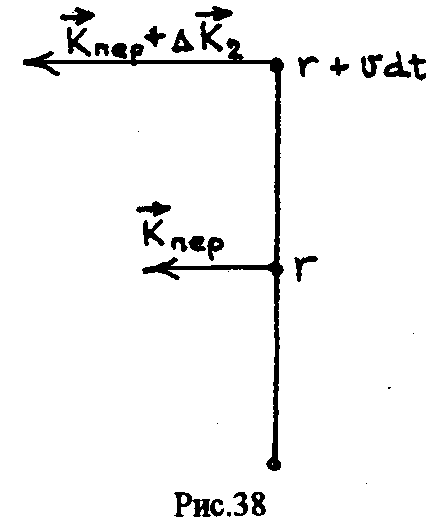оскольку тело движется равномерно относительно подвижной системы, будет изменяться только направление импульса. За промежуток времени система (и ее радиус) поворачивается на угол  = t (рис. 37).

П ри малых углах поворота вращение относительного импульса равно:

Н аправлено это изменение в сторону вращения перпендикулярно к радиусу. Переносный импульс направлен все время в сторону вращения перпендикулярно к радиусу, величина его, пропорциональная линейной скорости вращения системы, зависит от удаления от центра вращения (рис.38)

И зменение величины переносного импульса за время dt равно

К ак видно, изменения относительного и переносного импульсов одинаковы по величине и направлению, поэтому полное изменение импульса тела равно

С другой стороны, из основного закона динамики следует:

где F - равнодействующая приложенных к телу сил.

Таким образом, наблюдаемые изменения импульса вызываются внешними силами, равными по величине:F=2m

У читывая направления (рис. 39) векторов в векторном виде можно записать

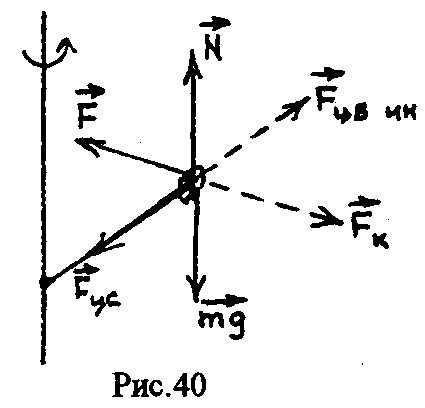
Д ля рассмотренного случая движения на рис.40 представим все действующие на тело силы. Пусть стержень вращается равномерно в горизонтальной плоскости, вдоль него равномерно движется небольшая муфточка. Относительно неподвижного наблюдателя на тело должны действовать следующие силы (отмеченные на рисунке сплошными линиями). Т.к. тело движется в горизонтальной плоскости, сила тяжести уравновешена реакцией стержня . Поскольку

траектория тела криволинейная, на него должна действовать центростремительная сила ,

о беспечивающая нормальное ускорение. Наконец, на тело действует рассмотренная выше сила , приложенная со стороны стержня.В системе, связанной с вращающимся стержнем, тело движется равномерно и прямолинейно, т.е. сумма приложенных к нему сил должна быть равной нулю. Как видно из рисунка, в горизонтальной плоскости силы не уравновешены, поэтому необходимо для выполнения законов динамики ввести силы инерции (на рисунке показаны пунктиром). Вдоль стержня действует центробежная сила инерции, уравновешивающая центростремительную силу.

С илу уравновешивает сила инерции Кориолиса

Как видно из (184), сила Кориолиса возникает во вращающейся системе отсчета при относительном движении тел. Исключением является движение тела вдоль оси вращения системы - силы инерции Кориолиса в этом случае не возникают.