3. Основные расчетные формулы Центрально-растянутые и центрально-сжатые элементы

Расчет на прочность элементов, подверженных центральному растяжению или сжатию силой , следует выполнять по формуле

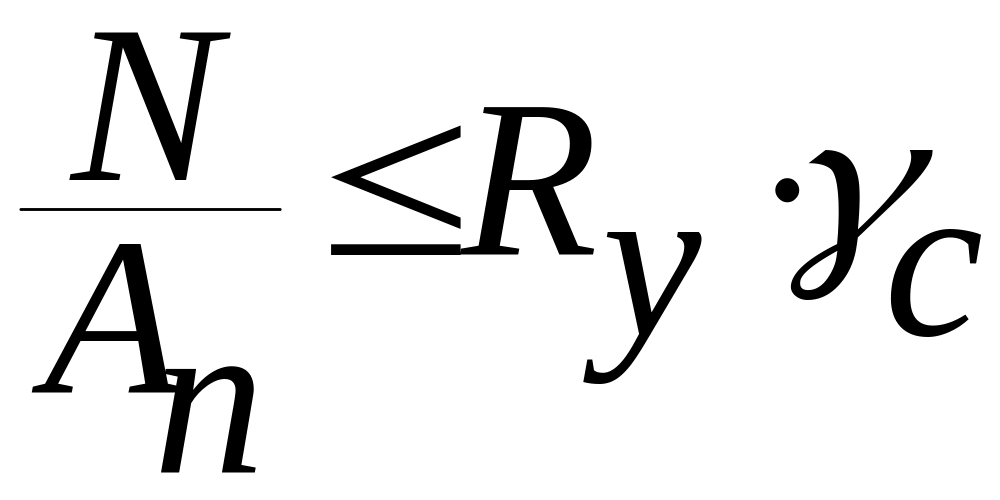
Расчет на прочность растянутых элементов конструкций из стали с отношением  , эксплуатация которых возможна и после достижения металлом предела текучести, следует выполнять по формуле

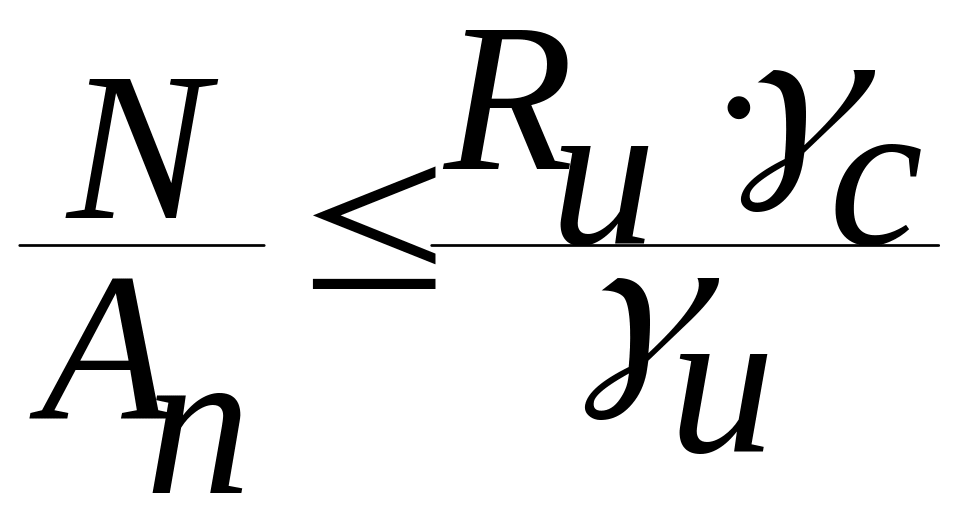
Расчет на устойчивость сплошностенчатых элементов, подверженных центральному сжатию силой , следует выполнять по формуле

.

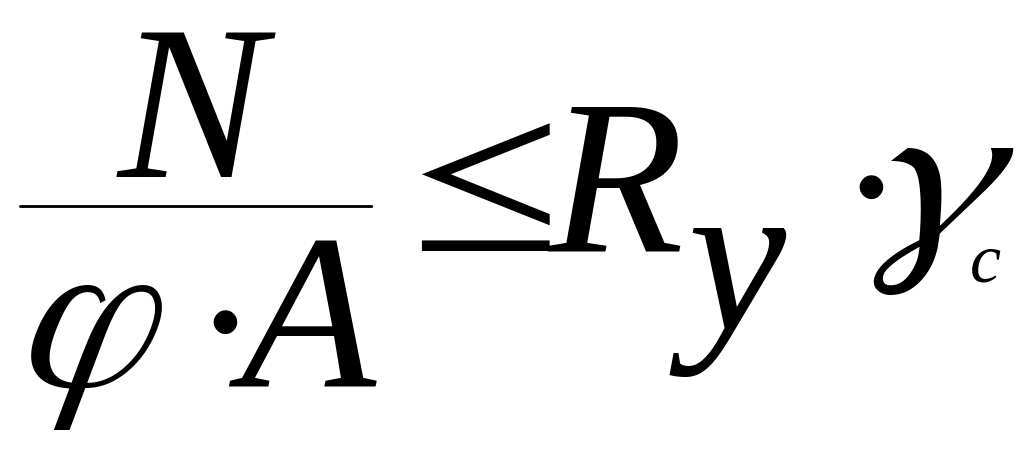Значения следует определять по СНиП в зависимости от гибкости .

Изгибаемые элементы

Расчет на прочность элементов (кроме балок с гибкой стенкой, с перфорированной стенкой и подкрановых балок), изгибаемых в одной из главных плоскостей, следует выполнять по формуле

.

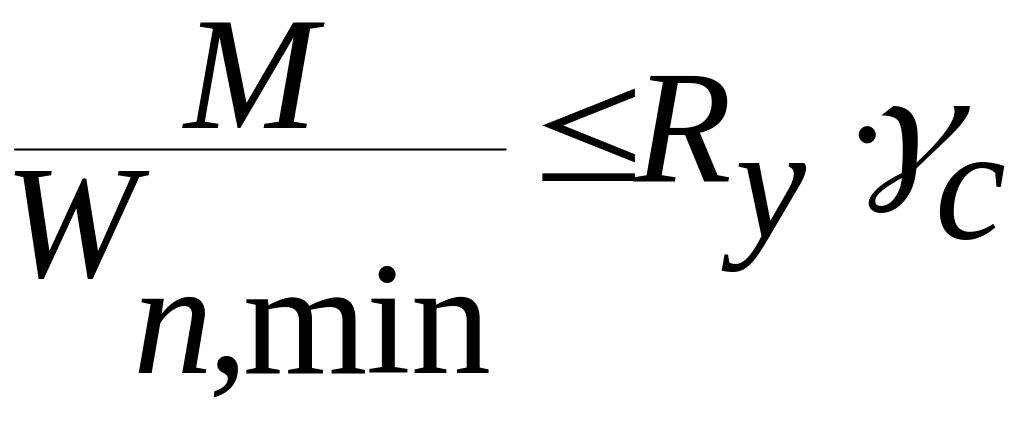Значения касательных напряжений в сечениях изгибаемых элементов должны удовлетворять условию

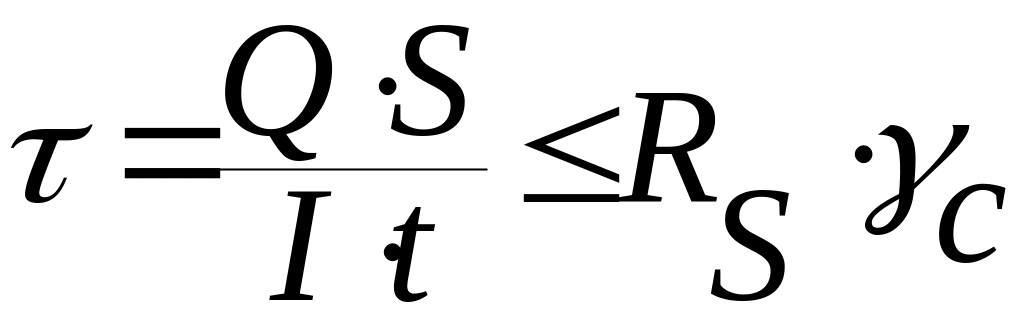
При наличии ослабления стенки отверстиями для болтов значения следует умножать на коэффициент , определяемый по формуле

,

где - шаг отверстий; - диаметр оверстия.

Для расчета на прочность стенки балки в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балки, не укрепленных ребрами жесткости, следует определять местное напряжение по формуле

= ,

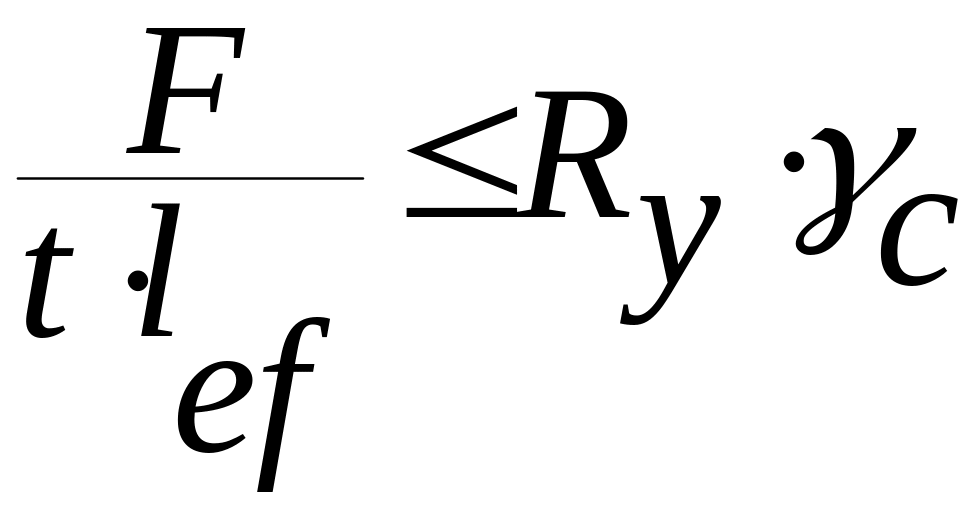где - расчетное значение нагрузки (силы);

- условная длина распределения нагрузки, определяемая в зависимости от условий опирания; например, для опирания на верхний пояс

,

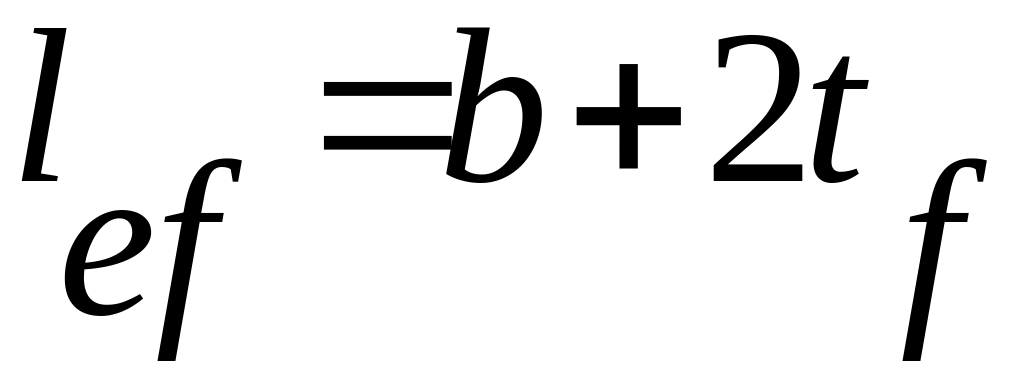где - толщина верхнего пояса балки.

Расчет на устойчивость балок двутаврового сечения, изгибаемых в плоскости стенки, следует выполнять по формуле

,

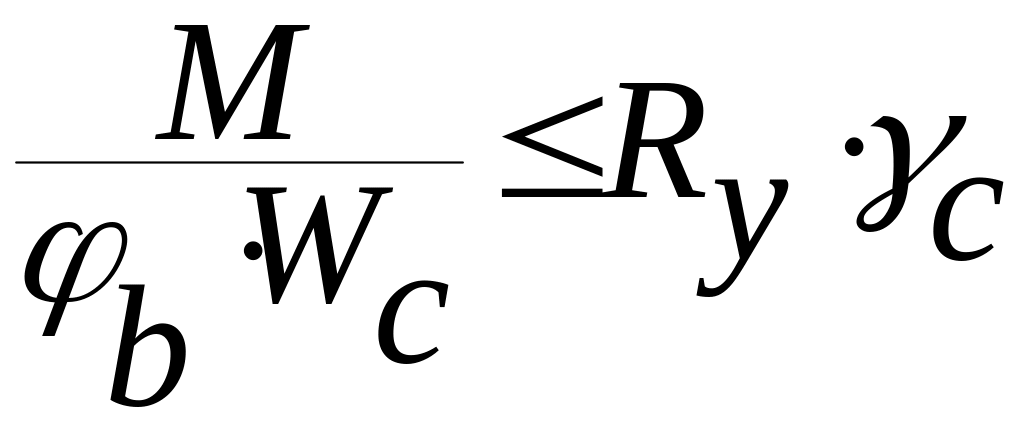где - следует определять для сжатого пояса; - следует определять согласно СНиП.

Устойчивость балок не следует проверять:

-при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (железобетонные плиты, плоский и профилированный металлический настил, волнистая сталь и т.п.);

-при отношении расчетной длины балки к ширине сжатого пояса , не превышающим значений, определяемых табличными формулами СНиП.

16). Потеря устойчивости центрально-сжатого стержня

Установившееся равновесие между внешними нагрузками (воздействиями) и внутренними усилиями называется напряженно-деформированным состоянием (НДС),

Предельные состояния жестких стержней определяются развитием пластических деформаций при достижении напряжениями предела текучести, а гибких стержней – потерей устойчивости.

Из курса сопротивления материалов известно, что при равенстве работы, совершаемой внешними силами, при сближении концов стержня сила достигает своего критического значения. При достижении силой критического значения прямолинейная форма стержня перестает быть устойчивой. Стержень изгибается в плоскости меньшей жесткости. Устойчивым состоянием будет новая криволинейная форма. При незначительном увеличении нагрузки искривление стержня начинает быстро нарастать, и стержень теряет несущую способность.

Для упругого стержня с шарнирно закрепленными концами критическая сжимающая сила определяется формулой Л. Эйлера

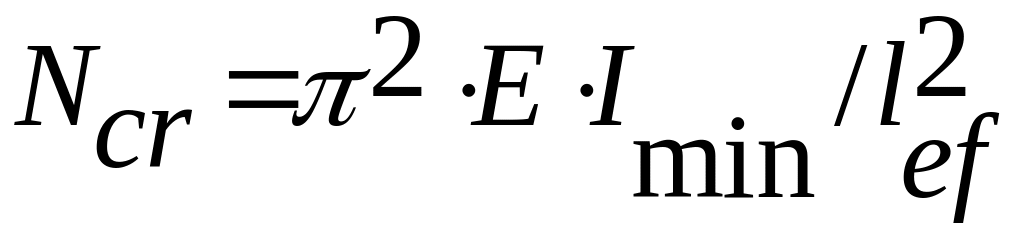. (7.1)

Соответственно критические напряжения

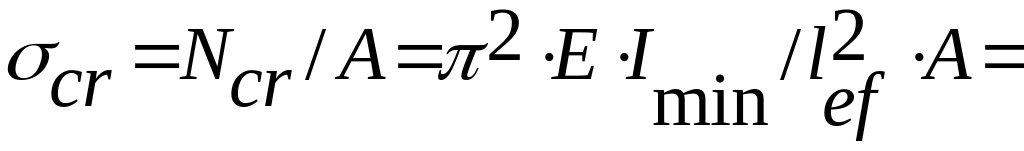
(7.2)

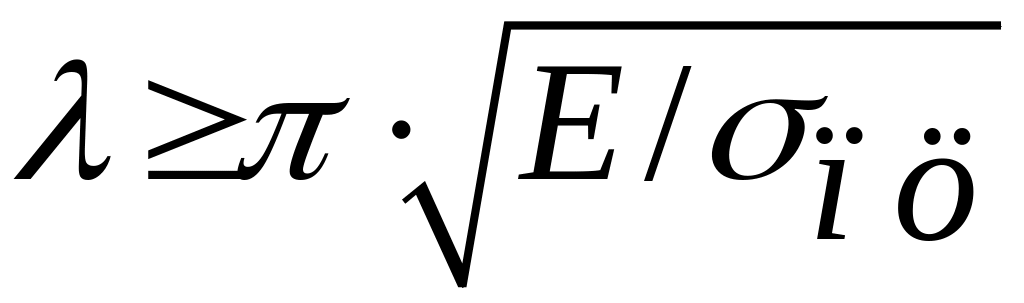Формула справедлива только при постоянном модуле упругости , в пределах упругих деформаций, т.е. при напряжениях, не превышающих предел пропорциональности, и . При средних и малых гибкостях стержня потеря его устойчивости происходит в упругопластической стадии работы материала при   .

Формула (7.2) показывает, что несущая способность стержня может быть увеличена путем увеличения момента инерции, без изменения площади поперечного сечения, путем размещения материала как можно дальше от главных осей инерции поперечного сечения. Поэтому трубчатые сечения наиболее экономичны, чем сплошные сечения. Уменьшая толщину стенки таких сечений и увеличивая поперечные размеры, можно повысить их устойчивость.

Эти рассуждения показывают, что устойчивость упругих систем или боковое выпучивание сжатых элементов имеет большое практическое значение. Это особенно справедливо во многих новейших конструкциях, в которых размеры поперечного сечения делаются все меньшими и меньшими благодаря использованию прочных материалов в целях экономии веса. Во многих случаях разрушение инженерных сооружений объясняется упругой неустойчивостью, а не недостаточной прочностью материала. При опытных исследованиях явления выпучивания сжатых стержней установлено, что связь между прогибом и нагрузкой зависит в значительной степени от точности, с какой центрирована нагрузка, и от прямизны и однородности стержня.