Нормальний розподіл

Неперервна випадкова величина має нормальний розподіл, якщо її функція щільності маж вигляд:

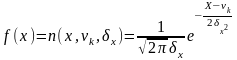, де – арифметичний корінь з дисперсії.

Функція розподілу:

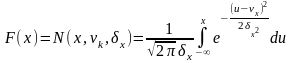
Перевіримо, що функція може бути функцією щільності неперервної випадкової величини.

Для цього треба показати, що вона є невід’ємна(виконується автоматично), , кусково-неперервна.

Перевіряємо інтеграл:

Розв’яжемо наступну задачу. Нехай є випадкова величина , в якої

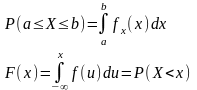
За означенням:

у звичайних функціях цей інтеграл не виражається. Виникає велика інженерна незручність, а саме: наша ймовірність залежить від чотирьох числових параметрів . Зміна значень хоча б одного з них вимагає знову використання чисельних методів для знаходження значень інтегрування.

Наслідок. Функція Лапласа.

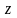
Числова скалярна функція дійсного аргументу 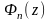зветься функцією Лапласа, якщо вона дорівнює:

Властивості функції Лапласа:

1. Якщо , то функція Лапласа дорівнює ймовірності попадання нормованої нормальної випадкової величини у відрізок

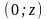
Випадкова величина зветься нормованою нормально, якщо її

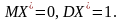
Для того щоб про нормувати довільну випадкову величину необхідно відняти від неї її математичне сподівання і поділити на її корінь з дисперсії:

Дійсно,

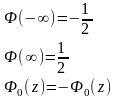
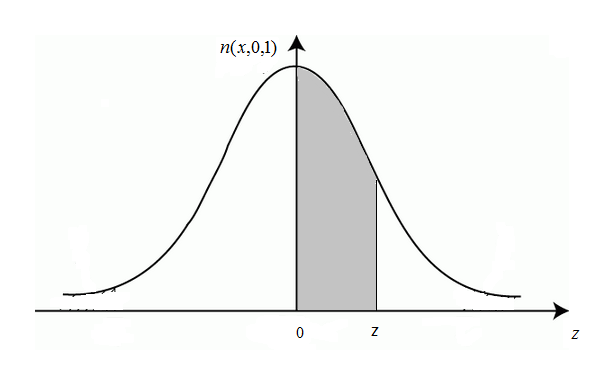
Функція Лапласа табульована, тобто існують таблиці для функції Лапаласа для дискретних значень із заданою похибкою знаходять значення функції.

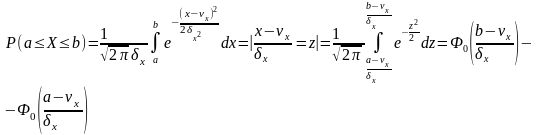
Нервіність Чебишева

Нехай невід’ємна випадкова величина тоді має місце нерівність

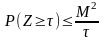
Виведення:

Примітка! Виведення для неперервного випадку, для дискретного вивести самим.

Функція щільності задана:

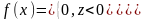
Знайдемо математичне сподівання

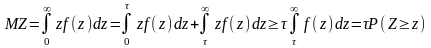
Примітка! Викинути І інтеграл, а у другому замінити на 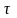і як константу винести.

Наслідок 1. Розглянемо поді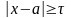ї і 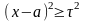. Ці події одинакові, значить у них одинакові ймовірності наставання, звідки:

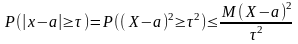
Наслідок 2. Якщо , то

Отримали результат з ймовірністю 1.

Двовимірні дискретні випадкові величини

Двовимірної дискретною випадковою величиною звуться дві дискретні випадкові величини кожна з яких задається табличкою.

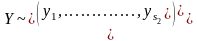
Двовимірна велична задається матрицею

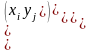У цій матриці деякі ймовірності можуть дорівнювати 0 (випадок, коли відповідна пара чисел принципово не може настати в наслідок випробувань).

Наприклад, попадання точки в коло заданого радіусу. Пари чисел з сірої області ніколи не можуть настати.

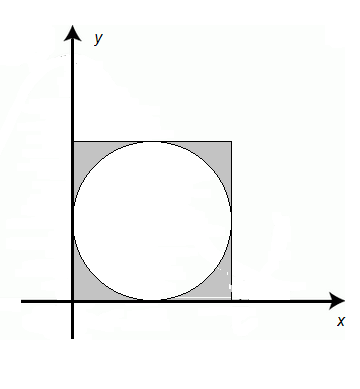о

Розглянемо події і

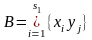
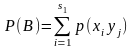
За побудовою

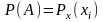
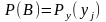
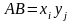– елементарна подія

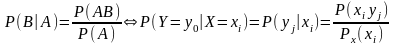
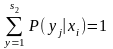Доведемо це.

Умовним математичним сподіванням зветься

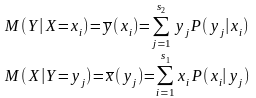
Умовною дисперсією зветься

Формально умовне сподівання і умовна дисперсія відрізняється від безумовних тим,що пишуть не безумовні ймовірності, а умовні ймовірності, а у дисперсії замість безумовного сподівання матсподівання – умовне.

Примітка! Функції 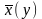, 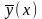звуться лініями регресії.

Якщо в цю функцію замість аргументів підставити елементарні події випадкової дискретної величини отримаємо умовні мат.сподівання при фіксованому значенні

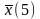– математичне сподівання випадкової величини , коли

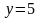
Звідси випливає зміст умовного математичного сподівання і дисперсії: умовне математичне сподівання – це число на числовій осі, відносно якого групуються результати конкретних випробувань над однією випадкової величиною при умові, що друга випадкова величина приймає одне стале фіксоване значення у достатньо великій серії випробувань.

А умовна дисперсія – це якісна міра ступеня концентрації цих результатів відносно математичного сподівання.(чим менша, тим сильніша).

Умовне математичне сподівання та умовна дисперсія використовуються для розв’язку наступної задачі, а саме там, де безумовна і умовна дисперсії різко відрізняються між собою.

Маємо двовимірну випадкову величину і обов’язково треба знати реалізацію як одної, так і другої. Але так трапилось, що знаємо результат тільки над однією випадковою величиною. Якщо умовна дисперсія дуже мала, то у якості вимірювань беремо її умовне математичне сподівання при тому значенні умовної величини, яке ми виміряли.