
- •Вступ у теорію ймовірностей
- •Частість наставання подій
- •Інженерний варіант аксіом Колмогорова
- •Умовна ймовірність
- •Незалежні події
- •Композиція двох випробувань
- •Композтція n випробувань
- •Випадкові величини
- •Початкові та центральні моменти дискретної випадкової величини
- •Розподіл Пуасона
- •І модель розподілу Пуасона.
- •Іі модель розподілу Пуасона.
- •Неперервні випадкові величини
- •Нормальний розподіл
- •Нервіність Чебишева
- •Двовимірні дискретні випадкові величини
- •Двовимірні неперервні випадкові величини
- •Багатовимірні дискретні випадкові величини
- •Неперервні випадкові величини
- •Функція коефіцієнт коваріації
- •Коефіцієнт кореляції
- •Теорема Бернуллі
- •Закон великих чисел
- •Класифікація збіжностей випадкових величин
- •Елементи математичної статистики
Неперервні випадкові величини
Простором елементарних подій неперервної випадкової величини є всі числа числової осі чи відрізок (відрізки) числової осі.
Як
розглядалось в прикладі ( кидання
навмання голки в пів інтервал
 )
ймовірність будь-якого числа, яке
теоретично може настати в результаті
випробування тотожно рівна 0. Таким
чином виникає ситуація, коли з’являються
елементарні чи складні події, що мають
ймовірність настання 0, а теоретично
можуть настати, і навпаки: є події, які
мають ймовірність наставання 1, а
теоретично можуть не настати. (Наприклад,
від всіх чисел числової осі викинути
всі раціональні числа).
)
ймовірність будь-якого числа, яке
теоретично може настати в результаті
випробування тотожно рівна 0. Таким
чином виникає ситуація, коли з’являються
елементарні чи складні події, що мають
ймовірність настання 0, а теоретично
можуть настати, і навпаки: є події, які
мають ймовірність наставання 1, а
теоретично можуть не настати. (Наприклад,
від всіх чисел числової осі викинути
всі раціональні числа).
Всі граничні теореми теорії ймовірностей і деякі просто результати гарантуються з ймовірністю 1, чи їх не наставання з ймовірністю 0. Як розв’язати це протиріччя між математичною теорією ймовірностей і інженерним трактуванням?
 ,
,
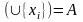
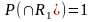
Як
і для будь-якої випадкової величини,
так і для неперервної випадкової величини
 функція
розподілу.
функція
розподілу.
її властивості збігаються з властивостями для дискретної випадкової величини, крім однієї: функція розподілу неперервної випадкової величини є неперервною функцією. Таким чином, якщо випадкова величина є неперервною, то нульова ймовірність наставання може бути лише у складних подій, що є нескінченно незліченою множиною чисел.

Неперервна
випадкова велична зветься абсолютно
неперервною
(далі в курсі просто неперервною), якщо
існує така числова скалярна функція
дійсного аргументу
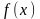 ,
що належить класу неперервних функцій
чи кусково-неперервних з обмеженою
кількістю розривів І роду, яка задовольняє
наступну інтегральну рівність:
,
що належить класу неперервних функцій
чи кусково-неперервних з обмеженою
кількістю розривів І роду, яка задовольняє
наступну інтегральну рівність:

Ця функція зветься функцією щільності (функцією густини). Прикладом неперервної випадкової величини, що не є абсолютно неперервною є сума неперервної випадкової величині і дискретної випадкової величини.
Властивості функції щільності

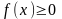 ,
тому що функція розподілу є монотонно
неспадна.
,
тому що функція розподілу є монотонно
неспадна.Нехай на відрізку функція щільності є неперервною функцією, тоді рівність еквівалентна
 ,
в тих точках, в яких ця похідна існує.
,
в тих точках, в яких ця похідна існує.Якщо існує похідна від функції розподілу, то має місце наступна рівність:
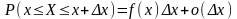
Доведення:
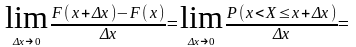 (використана
відповідна властивість функції розподілу)
(використана
відповідна властивість функції розподілу)

Примітка!
В
цьому виразі в якості
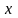 не
лівий кінець цього відрізка, а будь-яке
число цього відрізка. При цьому зміниться
лише конкретний вигляд нескінченно-малої
функції
не
лівий кінець цього відрізка, а будь-яке
число цього відрізка. При цьому зміниться
лише конкретний вигляд нескінченно-малої
функції
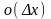
Приклади неперервних випадкових величин:
Рівномірний розподіл.
Неперервна
випадкова величина
рівномірно
розподілена на відрізку
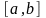 ,
якщо ї функція щільності наступна:
,
якщо ї функція щільності наступна:
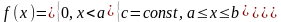
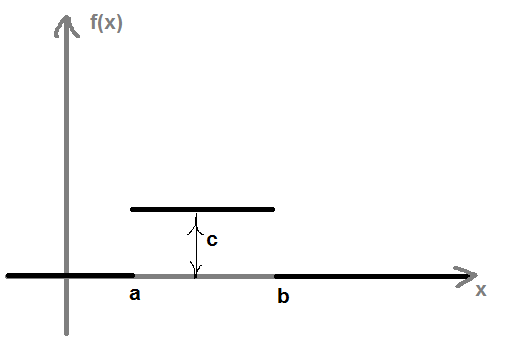
.
Знайдемо константу


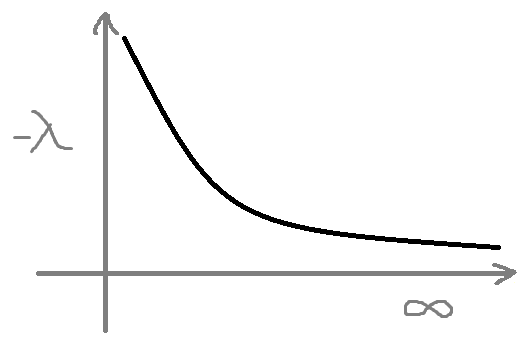
Експонційний розподіл
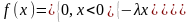
Самостійно
перевірити, що
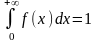
Математичне сподівання від неперервної випадкової величини
Нехай
 неперервна
випадкова функція дійсного аргументу
є
неперервна випадкова величина, у якої
відома функція щільності
.
Розглянемо випадкову величину
неперервна
випадкова функція дійсного аргументу
є
неперервна випадкова величина, у якої
відома функція щільності
.
Розглянемо випадкову величину
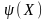 .
.
Наприклад,
 ш
ш
Математичним
сподіванням
 зветься
зветься

Обґрунтування цієї формули.
Ми знаємо, що якщо дискретна випадкова велична задається табличкою
 ,
то
,
то
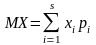 (для
спрощення вважаємо, що
є
неперервної на всій числовій осі.). Усю
числову вісь розіб’ємо на відрізки
довжини
,
–
мале число.
(для
спрощення вважаємо, що
є
неперервної на всій числовій осі.). Усю
числову вісь розіб’ємо на відрізки
довжини
,
–
мале число.
 –
лівий кінець і-ого
відрізка для будь-якого і
від
до
.
І замінимо неперервну випадкову величину
дискретною
випадковою величиною
–
лівий кінець і-ого
відрізка для будь-якого і
від
до
.
І замінимо неперервну випадкову величину
дискретною
випадковою величиною
 наступним
чином:
наступним
чином:
якщо неперервна випадкова величина настала в і-ий відрізок, то прийняла значення . Чим менше , тим краще апроксимує , при . переходить в .
Табличка для задається:
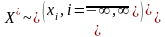
Неперервна
випадкова велична
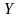 ,
що дорівнює
замінюється
дискретною випадковою величиною
,
що дорівнює
замінюється
дискретною випадковою величиною
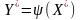
Так
як
–
неперервна числова скалярна функція
дійсного аргументу
,
то для малих
аргументу
,
то тим краще
 апроксимує
.
Якщо
переходить
в
.
апроксимує
.
Якщо
переходить
в
.
Знайдемо математичне сподівання для .
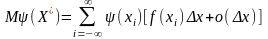
(використана
формула
 див. «початкові та центральні моменти
дискретної випадкової величини»).
див. «початкові та центральні моменти
дискретної випадкової величини»).
Якщо
цей інтеграл
існує, то
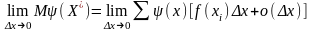 дорівнює
вищевказаному інтегралу
(обмежений
по модулю).
дорівнює
вищевказаному інтегралу
(обмежений
по модулю).
Математичним сподіванням неперервної випадкової величини зветься

Початковим моментом -ого порядку зветься
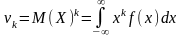
Показати
самим, що всі властивості початкових
моментів, включаючи
 такі
самі як і у дискретних випадкових
величин.
такі
самі як і у дискретних випадкових
величин.
Центральним моментом -ого порядку випадкової величини зветься
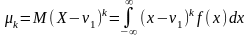
Дисперсією випадкової величини зветься її другий центральний момент

Довести самим, що всі властивості дисперсії випадкової величини, а саме:
, то

