Розподіл Пуасона

Є числова вісь, проведена нескінченна кількість випробувань, в кожному з яких випадковим чином з’являється число на числовій осі. Треба знайти ймовірність того, що на довільному відрізку довжини з’явиться чисел.

У такій загальній постановці задача не має розв’язку. Тому додається 3 умови.

1. Стаціонарність.

Ймовірність того, що на довільний відрізок числової осі попаде певна кількісь чисел залежить тільки від довжини відрізка і не залежить від того де він розташований на числовій осі.

2. Ординарність.

Ймовірність того, що на відрізок довжини 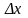попаде одне число є нескінченно мала порядку (поліном зі сталими коефіцієнтами, мінімальна ступінь при =1), а ймовірність попадання двох чи більше чисел є нескінченно малим більш високго порядку, ніж (мінімальна ступінь 2).

Якщо відрізок дуже малої довжини , то будемо вважати, що у нього може попасти одне число чи нічого. При цьому ми пприпускаємо помилку, але якщо 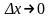, то отримаємо точний результат.

3. Безпіслядія.

Ймовірність того, що на довільний відрізок числової осі попаде певна кільістьчисел не залежить від того скільки чисел попало на відрізки, що не перетинаються з даним.

І модель розподілу Пуасона.

Внаслідок випробування з’являється число на числовій осі.

Візьмемо відрізок довжини 1 на числовій осі, зв’яжемо з цим відрізком випадкову величину (індекс зверху – довжина відрізка, з яким зв’язана випадкова величина)

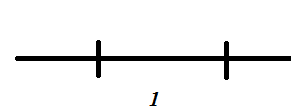: це кількість чисел, які попали у відрізок довжини 1 внаслідок проведеної нескінченної кількості випробувань. Це дискретна випадкова величина, що задається табличкою:

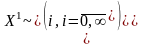
Позначимо

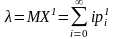
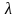– обмежене число чи нескінченність.

Беремо на числовій осі довільний відрізок довжини . (Самостійно довести, що 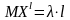. Примітка! Використати формулу, яка буде доведена далі: )

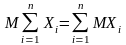Перший випадок. Довжина – ціле число.

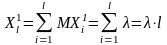
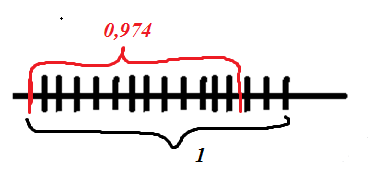
Другий випадок. Довжина – раціональне, з обмеженою кількістю занків після коми.

Наприклад, . Маємо довжин по 1 +

ділимо цей відрізок на 1000, отримуємо

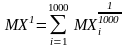
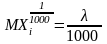
Для будь-якої кількості знаків після коми формула має місце, а, отже, існує граничний перехід.

Беремо довільний відрізок довжини , вибираємо достатньо велике число – натуральне: 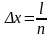було таким малим, щоб можна було застосувати умову ординарності (вважаючи, що на попадає одне число, чи нуль).

Розбиваємо відрізок на частин, зв’язуємо випадкову величину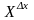 , тоді її можна задати табличкою

. Тому , де

Ймовірність того, що на відрізок довжини попаде рівно чисел дорівнює (використати умову безпіслядії) 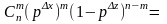(самостійно провести повний аналог між попаданням чисел на відрізок довжини і біномінальним розподілом. Аналог незалежних випробувань попадання чи непопадання числа в відрізок) = Спрямувавши , отримаємо:

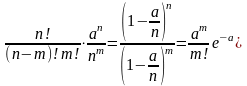
Перевірка

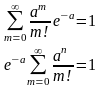, оскільки 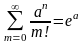, бо ця сума є розвиненням у ряд Маклорена

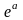
Іі модель розподілу Пуасона.

Розглянемо додатну числову вісь, на якій відмічаємо випадковий потік подій – це випадковим чином поява подій у часі. На відміну від першої моделі Пуасона, тут з’являється додаткова умова(*): кожна наступна подія випадково з’являється у часі, але не раніше, ніж з’явилися попередні події. На розподіл Пуасона накладаються умови:

1. Стаціонарність

2. Ординарність

3. Безпіслядія.

Розглянемо числовий відрізок довжини . Ймовірність того, що на часовому відрізку з’явились подій дорівнює

, де , 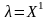. Тобто додаткова умова(*) не впливає на кінцевий резльтат.

У незалежних випробуваннях Бернуллі подія з’явиться разів, причому

– кількість випробувань дуже велике число

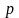– ймовірність дуже мале число, так щоб – не астрономічно велике.

Якщо – астрономічно велике, то за допомогою навіть суперсучасних комп’ютерів перетворити цей вираз у число неможливо, так як ! неможливо підрахувати, тому у якості наближення цього числа інженер бере:

ІІ модель розподілу Пуасона зветься законом рідких явищ.

Обґрунтування застосування формули Пуасона

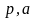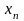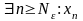Примітка! і – конкретні відомі нам числа. Залишаючи без зміни , спрямуємо до . Отримаємо числову послідовність, яка має границю: (див. Першу модель Пуасона, де ). Пригадаємо одне з означень теорії границь. Нехай числова послідовнсть має границю Це означає, що належить цьому околу. Якщо – кількість випробувань дуже велике число, то можемо припустити, що все це дорівнює дуже малому околу.