
- •Вступ у теорію ймовірностей
- •Частість наставання подій
- •Інженерний варіант аксіом Колмогорова
- •Умовна ймовірність
- •Незалежні події
- •Композиція двох випробувань
- •Композтція n випробувань
- •Випадкові величини
- •Початкові та центральні моменти дискретної випадкової величини
- •Розподіл Пуасона
- •І модель розподілу Пуасона.
- •Іі модель розподілу Пуасона.
- •Неперервні випадкові величини
- •Нормальний розподіл
- •Нервіність Чебишева
- •Двовимірні дискретні випадкові величини
- •Двовимірні неперервні випадкові величини
- •Багатовимірні дискретні випадкові величини
- •Неперервні випадкові величини
- •Функція коефіцієнт коваріації
- •Коефіцієнт кореляції
- •Теорема Бернуллі
- •Закон великих чисел
- •Класифікація збіжностей випадкових величин
- •Елементи математичної статистики
Початкові та центральні моменти дискретної випадкової величини
Дискретна випадкова величина задана табличкою:
Над
дискретною величиною
проведено
довільних
випробувань. Результатами випробувань
є числа, ї їх позначимо:
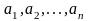 .
Візьмемо середнє арифметичне:
.
Візьмемо середнє арифметичне:
 Це
число має наступний зміст, а саме: воно
є центром
групування в результаті
проведених конкретних випробувань.
Це
число має наступний зміст, а саме: воно
є центром
групування в результаті
проведених конкретних випробувань.

Якщо
достатньо
велике число, то з закону великих
чисел:
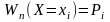
Математичним
сподіванням випадкової величини
зветься:

Примітка! Математичне сподівання чи математичне очікування (слова-синоніми)
З попередніх розмірковувань випливає наступний зміст математичного сподівання: це число на числовій осі, відносно якого групуються результати конкретних випробувань над випдковою величиною у довільній, достатньо великій серії випробувань.
Властивості математичного сподівання:

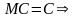 математичне
сподівання константи дорівнює константію.
Константу
можна представити як вироджену випадкову
величину, задавши табличку для неї
наступним
чином:
математичне
сподівання константи дорівнює константію.
Константу
можна представити як вироджену випадкову
величину, задавши табличку для неї
наступним
чином:

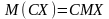 (Константа
виноситься з-під знака математичного
сподівання)
(Константа
виноситься з-під знака математичного
сподівання)
 Тоді
за загальною формулою
Тоді
за загальною формулою
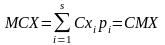
Самостійно
довести, якщо
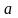 і
числа,
то
і
числа,
то
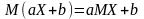
Розглянемо
будь-яку числову скалярну функцію
дійсного аргументу
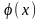

Якщо
у випробуванні настало
 ,
то
,
то


Ця
табличка не є табличкою
для випадкової величини
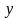 ,
бо у першому рядку числа можуть
повторюватись.
,
бо у першому рядку числа можуть
повторюватись.
Наприклад.
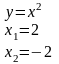
Щоб побудувати табличку для випадкової величини необхідно у першому рядку всі одинакові числа замінити одним і у відповідність йому поставити суму ймовірностей. А з цього випливає:

Початковим моментом -ого порядку випадкової величини зветься матиматичне сподівання у степені
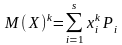
Три означення матиматичного сподівання:
Нехай
 ,
тоді
,
тоді
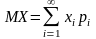 .
Математичне сподівання може бути:
обмежене по модулю,
.
Математичне сподівання може бути:
обмежене по модулю,
 чи
чи
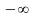 ,
невизначеним.
,
невизначеним.
Випадкова
велична
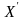 зветься
центровою випадковою величиною,
якщо
зветься
центровою випадковою величиною,
якщо
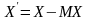


Центарльним
моментом
-ого
порядку
зветься математичне сподівання
центрованої величини
у
ступені
.

Дисперсією випадкової величини зветься її другий центральний момент

Характеристики дисперсії
Дисперсія є якісна характеристика ступеня концентрації результату конкретних випробувань над випадковою величиною відносно її математичного сподівання. А саме: чим менша дисперсія, ти м тісніше концентруються результати конкретних випробувань відносно математичного сподівання.
Дійсно, нехай дисперсія – це мале число. Це означає, що кожен доданок суми – дуже мале число. Розглянемо довільну елементарну подію, яка по модулю сильно відрізняється від математичного сподівання . Тоді ця (елементарна подія – )2 є дуже велике число, але відповідний доданок в сумі дуже малий. Це означає, що ймовірність наставання цієї події надзвичайно мале число. З цього випливає, що ця елементарна подія майже ніколи не буде наставати в результаті конкретних випробувань. Таким чином мати достатньо великі ймовірності наставання і часто наставати у результаті конкретних випробувань можуть тільки ті елементарні події, що по модулю мало відрізняються від математичного сподівання.
Формальні властивості дисперсії
 ,
то
,
то
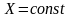
(Дану властивість довести самостійно)
 .
Якщо
,
то вона виноситься з-під знака дисперсії
у квадраті.
.
Якщо
,
то вона виноситься з-під знака дисперсії
у квадраті.
Доведення:

Доведення:

Доведення:

Твірна
функція
– математичне сподівання помножене на

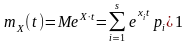
Твірна
функція завжди існує і є аналітичною,
якщо
– обмежене число. Якщо
– нескінченність, твірна функція може
бути обмеженою функцією дійсного
аргумента
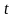 чи нескінченністю.
чи нескінченністю.
Властивості
Якщо твірна функція є аналітичною чи елементарною, то
 -ата
похідна при
-ата
похідна при
 -ий
початковий момент.
-ий
початковий момент.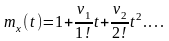
Доведення першої властивості
Якщо сума є аналітичною функцією, то -у похідну по можна внести під знак суми. З цього випливає перша власитвість і брати похідну від кожного доданку суми.
-ата похідна має вигляд
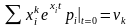
Доведення другої властивості:
Аналітична числова функція завжди розкладається в ряд Маклорена.
Наприклад. Твірна функція біномінального розподілу. Випадкова величина має біномінальний розподіл, якщо її елементарні події – це число появ події в незалежних випробуваннях Бернуллі. А ймовірність наставання цієї елементарної події дорівнює ймовірності наставання цього числа.

Знайдемо твірну функцію випадкової величини
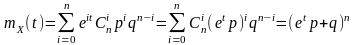
(Самостійно
довести, що у біномінальному розподілі
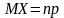 та
та
 .
При доведенні використати, що перша
похідна від твірної функції при
дорівнює
.
При доведенні використати, що перша
похідна від твірної функції при
дорівнює
 .
Для другої частини доведення взяти
другу похідну по
,
при
дорівнює
.
Для другої частини доведення взяти
другу похідну по
,
при
дорівнює
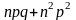 .
Врахувати, що
.
Врахувати, що
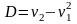 )
)





