Композтція n випробувань

Маємо простих випробувань

, де – номер випробування, – індекс елементарної події.

Композицією випробувань зветься складне випробування, що полягає у проведенні всіх простих випробувань.

За означенням елементарна подія композиційного випробування має загальний вигляд

Довжина

Якщо – простір елементарних подій -ого випробування.

– простір композиційного випробування

Прості випробування звуться незалежними, якщо

1. Ймовірність наставання подій композиційного випробування дорівнює добутку ймовірності наставання її компонент.

2. Прості випробування звуться незалежними, якщо в їх склад входять різні випадкові фактори, тобто жодні два випробування не містять спільного випадккового фактора.

Ці два означення еквівалентні, з 2 випливає 1.

Доведення базується на доведенні цього факту, коли 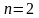, а далі принцип математичної індукції.

Наслідок:

Розглянемо , де – будь-яка складна подія, породжена і-им випробуванням.

Розглянемо

,

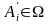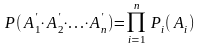
Ця формула формально використовується неправильно.

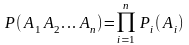
Внаслідок проведення незалежних випробувань (тобто будь-які 2 з яких не мають спільних випадкових факторів) ймовірність того, що у першому настане 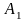, а у другом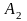у – , у – 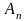дорівнює добутку ймовірності наставання цих подій.

незалежними випробуваннями Бернуллі зветься простих незалежних випробувань, в кожному з яких може настати подія чи . Ймовірність наставання події , 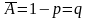. і можуть бути і неелементарними подіями.

Задача

Знайти ймовірність того, що в незалежних випробуваннях Бернуллі подія настає 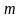разів, де .

Робимо композицію незалежних випробувань Бернуллі. Зафіксуємо загальний вигляд елементарної події композиційного випробування. Це буде символ довжини , що складається з простих символів, що є або .

Тоді

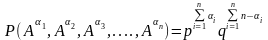
Подія, ймовірність якої шукаємо, є складною і складається з усіх різних елементарних подій, кожна з яких подію містить разів.

Ймовірність

, де – загальна кількість різних елементарних подій, що міститься разів.

Випадкові величини

Введення в теорію ймовірностей випадкових величин призвело до того, що ця наука стала необхідним інструментом в будь-якій області діяльності людини.

Випадкова величина задається випробуваннями, результатом якого є число. Таким чином, коли ми розглядаємо випробування, простором елементарних подій є сукупність чисел.

Розрізняють два типи випадкових величин:

• Дискретні

• Неперервні

Дискретною випадковою величиною зветься випадкова величина, простір елементарних подій якої є обмежена чи нескінченно злічена множина чисел.

Дискретна випадкова величина задається наступною табличкою:

, де задається для зручності у порядку зростання, і 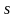– обмежене число чи . Перший рядок складають елементарні події,всі можливі числові. Другий – ймовірності наставання цих елементарних подій. З 3 аксіоми Колмогорова випливає, що

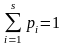
Неперервною випадковою величиною зветься випадкова величина, простір елементарних подій якої є вся числова всі, чи відрізок (відрізки) числової осі. Неперервна випадкова величина є математичною абстракцією, але без неперервних величин не існує жодної граничної теореми.

Функцією розподілу випадкової величини зветься числова скалярна функція дійсного аргументу 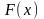, яка при будь-якому фіксованому значенні дорівнює ймовірності наставання наступної події:

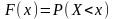
Ця рівність читається так: значення функції розподілу при фіксованому значенні аргументe дорівнює ймовірності наставання наступної події:

Внаслідок випробування випадкова величина 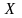приймає числове значення, яке строго менше фіксоване.

Примітка! (велика літера) – випадкова величина, (маленька літера) – аргумент її функції розподілу чи функції щільності.

Властивості функції розподілу

1. 

2. 

Для подій:

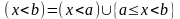так як ці дві події несумісні.

Розглянемо настeпуну частину прямої

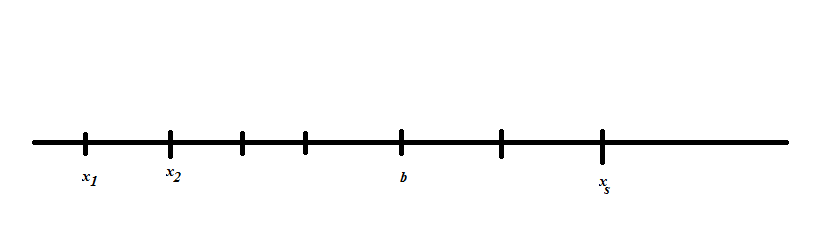
для дискретної випадкової величини простір елементарних подій складається з усіх елементарних , які менші

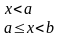
Тоді за 3 аксіомою Колмогорова отримаємо наступну рівність:

Доведення:

так як події несумісні.

З означення функції розподілу отримаємо .

Ймовірність того, що внаслідок випробування випадкова величина прийме значення, що належить інтервалу 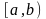дорівнює різниці значень функції розподілу на кінцях цього півінтервалу.

3. Функція розподілу – неспадна функція.

Із закону великих чисел випливає:

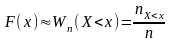
Побудуємо функцію розподілу для дискретної випадкової величини