Незалежні події

Незалежні події

Події і звуться незалежними, якщо: .

З цього означення випливає зміст терміну «незалежні події».

Нехай 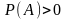, , 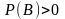тоді

Нехай навпаки:

Тоді:

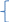
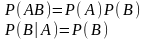
Доведення:

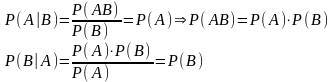
Аналогічно і для другої частини.

Таким чином отримали еквівалентні означення незалежності подій. Якщо , то і незалежні тоді, коли:

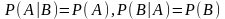
З еквівалентного означення незалежності і випливає: Подій і незалежні, якщо ймовірність наставання однієї з них не залежить від того настала чи не настала інша.

Якщо подій і незалежні, то незалежні також події

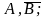
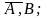
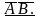
Доведення для :

Означення: Події звуться незалежними, якщо

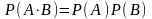
Незалежні сукупності:

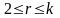Події називаються незалежними в сукупності, якщо для для

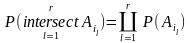
Якщо подій є незалежними в сукупності, то вони автоматично є незалежні. Зворотне твердження не вірне.

Нехай подій є незалежними в сукупності. Фіксуємо довільний набір індексів і беремо 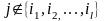. Знайдемо

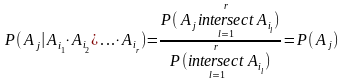
виконується 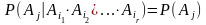, то це еквівалентне означення в сукупності.

Формула повної ймовірності

, ,

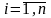
Події попарно не перетинаються

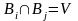
Події і зв’язані рівністю:

Знайдемо

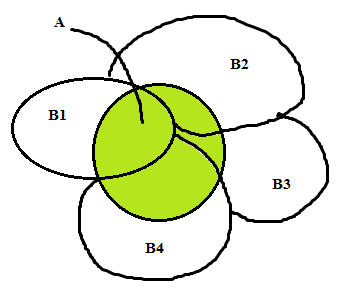
_{Яку б не взяли складну подію з} , вона обов’язково є у _{чи .}

_{Події попарно несумісні}

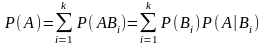
Приклад. Нехай маємо три склади урн: 7 урн першого типу, 4 урни другого типу та 6 урн третього типу. В кожній урні першого типу є 10 білих і 11 чорних кульок, у кожній урні другого типу – 5 білих і 10 чорних,, а в урнах третього типу – 3 білих і 7 чорних. Заплющивши очі навмання підійти до урни, перемішати кульки, вийняти 1 кульку, подивитись, кинути назад і перемішати знову.Знайти ймовірність того, що витягнута кулька біла.

Урни І типу 7 шт.	10 білих	11 чорних
Урни ІІ типу 4 шт.	5 білих	10 чорних
Урни ІІІ типу 6 шт.	3 білі	7 чорних

Елементарні події – усі кульки, _{– всі білі кульки, 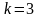– кількіть різних типів урн, 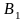– всі кульки, що входять в 7 урн першого типу.}

_{– всі кульки, що входять в 4 урни другого типу.}

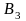_{– всі кульки, що входять в 6 урн третього типу.}

_{Всі події попарно несумісні, тому:}

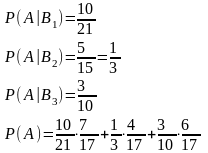
_{Приклад. Та сама постановка задачі, що і у прикладі, наведеному вище. Треба знайти у результаті випробування з’явилась біла кулька, знайти ймовірність того, що вона витягнута з урни -ого складу.}

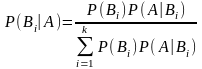
_{Знайти 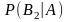з попереднього прикладу.}

Композиція двох випробувань

_{Простим випробуванням зветься випробування, яке не можна розкласти на компоненти чи більш детальні випробування}

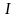_{випробування 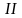випробування}

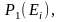
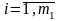
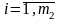
_{Складним або композицією двох простих випробувань зветься проведення як першого, так і другого випробування.}

_{У цьому означенні не фіксується час проведення випробування. Це задається конкретною задачею.}

_{Наприклад, випробування — підкидання монети.}

_{випробування — підкидання шестигранного кубика.}

_{Побудуємо простір елементарних подій композиційного випробування , де о—випадання орла, р – випадання решки. Та друге випробування , де 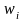– випадання і-ої грані.}

_{Нехай – простір елементраних подій композиційного випробування.}

_{, де} – декартовавий добуток.

_{У загальному випадку 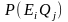не задається.}

_{Так як,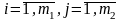} , то можливх пар усього

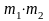
Пояснення цього факту наведено на двох прикладах.

_{Приклад 1}

_{Перше просте випробування – підкидання кубика, друге випробування – підкидання кубика.}

_{Для першого 1/6}

_{Для другого 1/6}

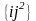
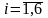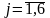_{, Усього отримаємо 6 6=36}

_{Йовірність наставанян кожної пари = 1/6, всі інші події мають ймовірність наставння рівну тотожному 0.}

_{Приклад 2}

_{Той самий перший приклад, але кубики підкидають дві різні людини.}

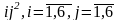_{Отримаємо 1/36.}

_{Таким чином не знаходиться у загальному випадку, тому що і не показують, які випадкові фактори входять у перше і друге просте випробування, і як вони взагалі зв’язані між собою.}

_{Випадкові фактори, що входять у перший приклад одинакові, а в другому – різні, тобто нема жодного випадкового фактора, що одночасно входить в одне і друге випробування.}

_{Два простих випробування звуться стахистично (випадково) зв’язаними, якщо в їх склад входять однакові випадкові фактори, але також входять і різні.}

_{Два прості випробування зв’язані функціонально, якщо в їх склад входять однакові випадкові фактори. ( Приклад 1).}

_{Два прості випробування звуться незалежними, якщо в їх склад входять різні випадкові фактори.}

_{Розглянемо подію}

_Нехай

Задамо подію

настає, коли в першому випробування настала елементрана подія

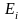
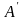настає, коли в наслідок проведення композиційного випробування в першому простому випробування настала , а в другому будь-яка.

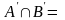елементарна подія, що складається з єдиної події

Подія настає, коли у другому випробуванні настає

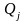
Подія 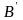настає, коли у другому випробуванні настає , а у першому будь-яка елементарна подія.

Узагальнення означення і для

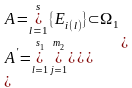
Дійсно, подія настає, коли у першому випробуванні настала елементарна подія, що входить в склад

настає, коли внаслідок проведення складного випробування, коли у першому настала подія , а у другому будь-яка. Тобто настає тоді і тільки тоді, коли настала подія з .

Провели композиційних випробувань. І нехай з цих випробувань у настала , тобто у кожному з цих композиційних випробувань у другому простому випробуванні настала подія .

Нехай у 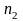настала подія . У кожному з композиційних випробувань у другому простому випробуванні настала подія , а у першому . Тоді за побудовою умовна частість дорівнює

Так як ймовірність по Колмогорову – це кількісна міра частості

Розглянемо композиційних випробувань, і відкинемо друге просте випробування. Залишимо повторів першого випробування і випробування, у кожному з яких настала . Так як перше і друге просте випробування не мають спільних випадкових факторів, то це означає, що для першого випробування його повторів є довільним випробуванням (те що у другому випробуванні настає подія не накладає жодних умов на результат першого випробування). Тоді для першого випробування дріб є частістю наставання безумовної події в довільній серії випробувань. Кількісна міра цієї частості дорівнює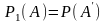 . З цього випливає, що події і – незалежні, бо ми показали, що

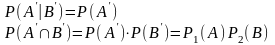
_{Повертаємось до випадку , коли та}

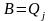
Таким чином довели еквівалентність означень.

Отриманий результат на практиці використовується формально невірно.

Нехай події незалежні за означенням: ,

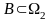
Ймовірність того, що у першому випробуванні настане , а у другому дорінює

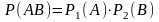, що формально невірно, оскільки запис не має змісту, бо і належать різним просторам елементарних подій.