Закон великих чисел

Маємо необмежену послідовність незалежних довільно, але однаково розподілених випадкових величин з 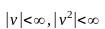. Якщо дві випадкові величини мають однаковий розподіл, то у них одинакові математичні сподівання і дисперсії. Показати самим, що

Спрямуємо до нескінченності.

Використовуючи розмірковування приведені в кінці теореми Бернуллі (стандартний прийом математичної статистики) є одне фізично-існуюче випробування, що породило фізично-існуючу випадкову величину . разів повторили випробування і зафіксували результати у кожному повторі, тоді середнє арифметичне цих результатів при достатньо великій кількості повторів випробувань наближено дорівнює мат. сподіванню фізично-існуючої величини .

Класифікація збіжностей випадкових величин

Послідовність випадкових величин по ймовірності збігається до випадкової величини , якщо існує наступний ліміт

Приклад 1. Теорема Бернуллі.

_{Послідовність випадкових величин} при по ймовірності збігається до числа _.

Приклад 2. Закон великих чисел

Довести, що послідовність випадкових величин 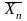по ймовірності збігається до константи , що є її математичним сподіваннм. 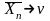при

Збіжність середньоквадратичних

Послідовність випадкових величин збігається до випадкової величини середньоквадратичної, якщо існує ліміт:

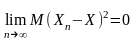
Покажемо, що збіжність середньоквадратичних принаймні не гірша, ніж збіжність по ймовірності: якщо існує збіжність середньоквадратичного, то існує збіжність по ймовірності.

Доведення:

Запишемо нерівність Чебишева

. Тоді спрямуємо до нескінченності. . Із ланцюжка нерівностей отримаємо збіжність по ймовірності. (Довести самостійно).

Збіжність по розподілу

Маємо послідовність випадкових величин . Побудуємо відповідну послідовність їх функцій розподілу. . Нехай ця послідовність слабо збігається до функції , що є функцією розподілу випадкової величини . Тоді кажуть, що послідовність випадкових величин збігається по розподілу до випадкової величини .

Примітка! Слаба збіжність – це збіжність функції до функції в кожній точці її неперервності (якщо – неперервна, то слаба збіжність – просто збіжність).

Наслідок. Якщо 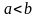, і – точки, в яких функція – неперервна, існує ліміт:

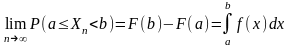
Примітка! Друга рівність має місце тільки тоді, коли існує

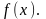
Центральна скалярна гранична теорема

(частковий випадок) дається без доведення.

Маємо послідовність незалежних довільно, але однаково розподілених випадкових величин

, у яких ,

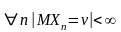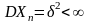
Примітка! На екзамені показати самим, що якщо дві випадкові величини однаково розподілені, то у них однакове математичне сподівання і однакова дисперсія.

Розглянемо послідовність випадкових величин

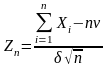
– послідовність нормованих сум . Тоді при послідовність випадкових величин по розподілу збігається до нормованої нормально розподіленої випадкової величини , то мажмо не слабу збіжність, а просто збіжність, тобто:

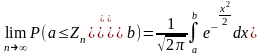
Примітка! Для строгого доведення цієї теореми потрібно знати властивості характеристичної функції 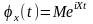, де

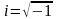
Наслідок 1. Теорема Муавра-Лапласа – частковий випадок центральної граничної теореми.

Послідовність нормованих сум по розподілу збігається.

Наслідок 2. Так як в центральній граничній теоремі сума нормується лише для того, щоб на нескінченності не мати нескінченних параметрів,

• то центральна гранична теорема застосовується, коли доданків не менше 20-40

• то для обмеженого можна не нормувати суму.

Приклад. Для

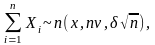а випадкова величина

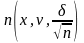
Наслідок 3. Є фізичне одне випробування . Провели повторів і зафіксували результат 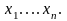Тоді використовуючи наслідок теореми Бернуллі число можна вважати реалізацією , де – незалежні віртуальні копії фізично-існуючої випадкової величини .

Загальний випадок центральної граничної теореми (дається без доведення і в інженерній інтерпретації)

Маємо достатньо велику кількість (на практиці 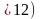незалежних довільно і неоднаково розподілених випадкових величин, які у випробуваннях приймають значення одного порядку (жодна з випадкових величин не домінує над іншою) тоді їх сума розподілена нормально.

Наслідок. Покажемо, що інтегральна похибка вимірювань є сумою 8-12 незалежних складових, кожна з яких не домінує над іншою. (виконується загальний варіант центральної граничної теореми).