Вступ у теорію ймовірностей

Теорія ймовірностей виникла як наука з впевненості в тому, що за можливими випадковими явищами ховаються детерміновані закономірності.

І саме ці закономірності і вивчає теорія ймовірностей.

Наприклад. Підкидуємо монету. Монета може впасти на землю орлом чи решкою. Ймовірність випадання тої чи іншої сторони дорівнює .

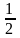Теорія ймовірностей , як і кожна наука, базується на первісних означеннях.

Мовою теорії ймовірностей є теорія множин.

Випробування інверсії.

Реалізація певного комплексу умов, що може повторюватись необмежену кількість разів, у цей комплекс умов входять випадкові фактори, реалізація яких випробуваннями і приводить до неоднозначності результату випробування.

Елементарною подією зветься конкретний результат випробування.

Простором елементарних подій називається множина(сукупність) всіх різних елементарних подій, що породжуються даним випробуванням.

Наприклад. Підкидання шестигранного кубика.

– випадання грані з 1.

– випадання грані з 2.

– випадання грані з 3.

– випадання грані з 4.

– випадання грані з 5.

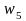– випадання грані з 6.

Тоді

Складною подією зветься підмножина .

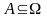Наприклад. 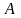– випадання грані з парним числом.

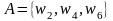
У випробуванні складна подія настає тоді і тільки тоді, коли внаслідок випробування настає елементарна подія, яка входить у склад .

Таким чином в результаті проведеного випробування настають всі різні складні події, в кожну з яких входить елементарна подія, що настала внаслідок випробування.

Вірогідною(достовірною) зветься подія, яка завжди настає.

– неможлива подія, тобто та, яка ніколи не настає у результаті випробування.

Ø

Операції над подіями

Операція об’єднання

Подія 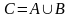, якщо подія складається з усіх елементарних подій, що входять в подію , в подію , чи і одночасно.

Примітка! Якщо елементарна подія входить і в , і одночасно, то у вона входить тільки один раз.

Означення об’єднання подій поширюється на довільну кількість подій.

– це обмежена чи нескінченно-злічувана множина.

Потужності обох відрізків рівні.

настає випробуванням, якщо настала хоча б одна з подій .

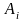Операція перетину

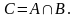( ) є перетином і , якщо складається з усіх елементарних подій і , і

настає випробуванням тоді і тільки тоді, як настала подія і , і .

1. 2)

3. 

Різниця множин

. ( )

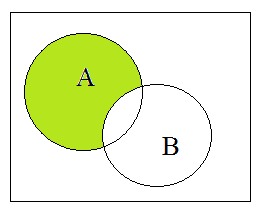
– подія протилежна

Події і звуться несумісними, якщо їх перетин:

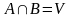
Наслідок: якщо події і несумісні, то вони ніколи не можуть настати внаслідок одного випробування.

=

=

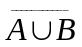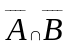
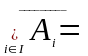
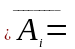
Частість наставання подій

– множина всіх підмножин

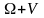
Елементів у

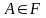
– усі випробування.

– кількість випробувань, у кожному з яких настала подія А.

Частістю наставання

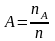
Властивості частості:

1. 

2. 

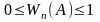
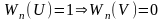
3. Розглянемо ,

Розглянемо попарно несумісних подій такі що, 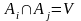для

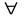
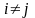
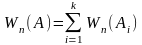
Нехай настала , тоді жодна не настала .

Теорія ймовірностей описує не будь-які випробування, а тільки ті, для яких виконується, що у будь-якій довільній серії випробувань, для будь-якої події частість наставання події при необмеженій кількості випробувань ( 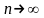) завжди існує один той самий lim, слушно назвати ймовірністю наставання події .

Наслідок. З цього випливає інженерне розуміння події.

Ймовірність наставання події – це частість наставання події при достатньо великій кількості випробувань.

Ймовірність наставання події – це границя частості наставання події у довільній, необмеженій серії випробувань.

Довільна серія випробувань означає, що на результат випробувань не накладено жодних умов.

Але всі спроби побудувати теорію ймовірностей як математичну науку, що використовує означення ймовірності : виявились неможливі.

Найвдаліша спроба належить американському вченому Мізесу, але математики його теорію не сприйняли. Вихід з положення знайшов видатний радянський вчений академік Колмогоров. Саме він побудував математичну теорію ймовірностей, яку прийняв світ. Він ввів аксіоматичні ймовірності наставання події, з яких прямо не випливає, що ймовірність наставання події – це границя частості наставання події. Цей результат існує, є теоремою і доводиться.