3.3.1. Аналіз моделі на чутливість
На малюнку 3.4 зображено Excel-звіт – звіт про стійкість.
Рисунок 3.4. Excel-звіт – звіт про стійкість
На малюнку 3.5 зображено Excel-звіт – звіт про границі.
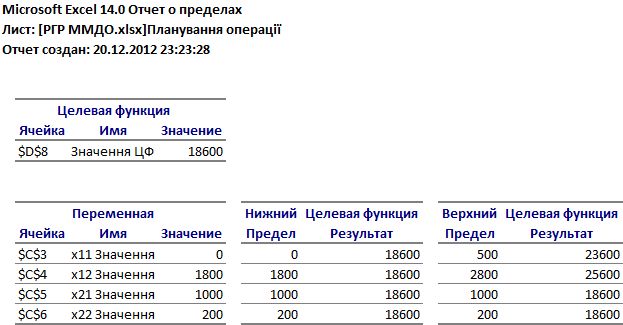
Рисунок 3.5. Excel-звіт – звіт про границі
3.4. Рішення задачі симплекс-методом
min z = 10*x11 + 7*x12 + 5*x21 + 5*x22
0.5*х11 + 0.25*х12 <= 700
1*x21 + 0.5*x22 <= 1100
x11 + x21 >= 1000
x12 + x22 >= 2000
x11, x12, x21, x22 >= 0
min z = 10*x11 + 7*x12 + 5*x21 + 5*x22 + 0*s1 + 0*s2 + 0*S3 + 0*S4 + 0*R1 + 0*R2
0.5*х11 + 0.25*х12 + s1 = 700
1*x21 + 0.5*x22 + s2 = 1100
x11 + x21 - S3 + R1 = 1000
x12 + x22 - S4 + R2 = 2000
x11, x12, x21, x22, s1, s2, S3, S4, R1, R2 >= 0
min r = R1 + R2
R1 = 1000 - x11 - x21 + S3
R2 = 2000 - x12 - x22 + S4
r = 1000 - x11 - x21 + S3 + 2000 - x12 - x22 + S4 = 3000 - x11 - x12 - x21 - x22 + S3 + S4
r + x11 + x12 + x21 + x22 - S3 - S4 = 3000
z - 10*x11 - 7*x12 - 5*x21 - 5*x22 - 0*s1 - 0*s2 - 0*S3 - 0*S4 - 0*R1 - 0*R2 = 0
БЗ |
x11 |
x12 |
x21 |
x22 |
s1 |
s2 |
S3 |
S4 |
R1 |
R2 |
Ріш. |
Відн. |
r |
1 |
1 |
1 |
1 |
0 |
0 |
-1 |
-1 |
0 |
0 |
3000 |
|
z |
-10 |
-7 |
-5 |
-5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
s1 |
0,5 |
0,25 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
700 |
- |
s2 |
0 |
0 |
1 |
0,5 |
0 |
1 |
0 |
0 |
0 |
0 |
1100 |
2200 |
R1 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
1 |
0 |
1000 |
- |
R2 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
1 |
2000 |
2000 |
БЗ |
x11 |
x12 |
x21 |
x22 |
s1 |
s2 |
S3 |
S4 |
R1 |
R2 |
Ріш. |
Відн. |
r |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
0 |
-1 |
1000 |
|
z |
-10 |
-2 |
-5 |
0 |
0 |
0 |
0 |
-5 |
0 |
5 |
10000 |
|
s1 |
0,5 |
0,25 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
700 |
- |
s2 |
0 |
-0,5 |
1 |
0 |
0 |
1 |
0 |
0,5 |
0 |
-0,5 |
100 |
100 |
R1 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
1 |
0 |
1000 |
1000 |
x22 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
1 |
2000 |
- |
БЗ |
x11 |
x12 |
x21 |
x22 |
s1 |
s2 |
S3 |
S4 |
R1 |
R2 |
Ріш. |
Відн. |
r |
1 |
0,5 |
0 |
0 |
0 |
-1 |
-1 |
-0,5 |
0 |
-0,5 |
900 |
|
z |
-10 |
-4,5 |
0 |
0 |
0 |
5 |
0 |
-2,5 |
0 |
2,5 |
10500 |
|
s1 |
0,5 |
0,25 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
700 |
1400 |
x21 |
0 |
-0,5 |
1 |
0 |
0 |
1 |
0 |
0,5 |
0 |
-0,5 |
100 |
- |
R1 |
1 |
0,5 |
0 |
0 |
0 |
-1 |
-1 |
-0,5 |
1 |
0,5 |
900 |
900 |
x22 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
1 |
2000 |
- |
БЗ |
x11 |
x12 |
x21 |
x22 |
s1 |
s2 |
S3 |
S4 |
R1 |
R2 |
Ріш. |
Відн. |
r |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
|
z |
0 |
0,5 |
0 |
0 |
0 |
-5 |
-10 |
-7,5 |
10 |
7,5 |
19500 |
|
s1 |
0 |
0 |
0 |
0 |
1 |
0,5 |
0,5 |
0,25 |
-0,5 |
-0,25 |
250 |
|
x21 |
0 |
-0,5 |
1 |
0 |
0 |
1 |
0 |
0,5 |
0 |
-0,5 |
100 |
|
x11 |
1 |
0,5 |
0 |
0 |
0 |
-1 |
-1 |
-0,5 |
1 |
0,5 |
900 |
|
x22 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
1 |
2000 |
|
БЗ |
x11 |
x12 |
x21 |
x22 |
s1 |
s2 |
S3 |
S4 |
R1 |
R2 |
Ріш. |
Відн. |
z |
0 |
0,5 |
0 |
0 |
0 |
-5 |
-10 |
-7,5 |
|
|
19500 |
|
s1 |
0 |
0 |
0 |
0 |
1 |
0,5 |
0,5 |
0,25 |
-0,5 |
-0,25 |
250 |
- |
x21 |
0 |
-0,5 |
1 |
0 |
0 |
1 |
0 |
0,5 |
0 |
-0,5 |
100 |
- |
x11 |
1 |
0,5 |
0 |
0 |
0 |
-1 |
-1 |
-0,5 |
1 |
0,5 |
900 |
1800 |
x22 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
1 |
2000 |
2000 |
БЗ |
x11 |
x12 |
x21 |
x22 |
s1 |
s2 |
S3 |
S4 |
R1 |
R2 |
Ріш. |
Відн. |
z |
-1 |
0 |
0 |
0 |
0 |
-4 |
-9 |
-7 |
|
|
18600 |
|
s1 |
0 |
0 |
0 |
0 |
1 |
0,5 |
0,5 |
0,25 |
-0,5 |
-0,25 |
250 |
|
x21 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
1 |
0 |
1000 |
|
x12 |
2 |
1 |
0 |
0 |
0 |
-2 |
-2 |
-1 |
2 |
1 |
1800 |
|
x22 |
-2 |
0 |
0 |
1 |
0 |
2 |
2 |
0 |
-2 |
0 |
200 |
|
Симплекс-таблиця є оптимальною.
x11 = 0
x12 = 1800
x21 = 1000
x22 = 200
z = 18600