МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ПАВЛОГРАДСЬКИЙ ТЕХНІКУМ

ДЕРЖАВНОГО ВНЗ «НГУ»

Методичні інструкції

по виконанню самостійних робіт з теми

«Логічні фрагменти інтегрального виконання»

Дисципліна «Комп’ютерна логіка»

Напрямок підготовки 050102 „Комп’ютерна інженерія”

Спеціальність 5.05010201 «Обслуговування комп’ютерних

систем і мереж»

Павлоград

2012

Методичні інструкції

по виконанню самостійних робіт з теми

«Логічні фрагменти інтегрального виконання»

Дисципліна «Комп’ютерна логіка»

Напрямок підготовки 050102 „Комп’ютерна інженерія”

Спеціальність 5.05010201«Обслуговування комп’ютерних систем і

мереж»

розроблено: Кондратова О.Л. викладач

Розглянуто та схвалено на засіданні циклової комісії комп'ютерних технологій

Протокол № від

Голова ц/к _____________

О.В. Демченко

Пояснювальна записка

В посібнику приведений в стислому вигляді теоретичний матеріал до вивчення розділу «Логічні фрагменти інтегрального виконання» з дисципліни «Комп’ютерна логіка», а також завдання до кожної теми.

Посібник може використовуватись студентами для самостійного засвоєння матеріалу лекцій та самостійних робіт, а також на уроці в якості опорного конспекту лекцій.

Основна мета створення посібника – спростити для студентів процес підбору необхідного теоретичного матеріалу для самостійного засвоєння, полегшити та оптимізувати роботу викладача при викладенні матеріалу, вирішити питання недостатньої кількості підручників.

1

Самостійна робота № 14

Тема: Побудова комбінаційної схеми з логічних елементів на основі рівняння алгебри логіки

Мета: Закріпити набуті знання та навички, перевірити їх при виконанні практичних завдань.

Завдання

1. Засвоїти теоретичний матеріал згідно теми;

2. Дати відповіді на поставлені питання (лекція 16);

3. Виконати письмово приведені завдання;

4. Випишіть питання, що виникли в ході засвоєння матеріалу;

5. Зробіть висновки.

Рекомендована література:

1. М.Ф. Бондаренко, Н.В. Білоус, А.Г.Руткас. Комп’ютерна дискретна математика. – Х: „Компанія СМІТ”, 2004.-480с.

2. Стрыгин В.В., Щарев Л.С. Основы вычислительной микропроцессорной техники и программирования: Учеб. для вузов. – М: Высш. Шк., 1989. – 479с.

Логічні схеми

Логічні схеми у комп’ютерах та інших електронних пристроях оперують з наборами вхідних та вихідних даних, що складаються з нулів і одиниць. Булева алгебра і булеві функції зображують математичний апарат для роботи з такими даними і використовуються для аналізу та синтезу логічних схем (ланцюгів). Основою побудови логічних схем є набір логічних елементів.

Таблиця 1 Основні логічні елементи

Назва	Символ логічних елементів	Вітчизняні позначки	Булева функція
І			Кон’юнкція
АБО			Диз’юнкція
НЕ		x1	Інверсія
І-НЕ			штрих Шеффера

2

АБО-НЕ					Стрілка Пірса
ВИКЛЮЧНЕ АБО			ХОР =

Кожний логічний елемент реалізує деяку логічну функцію. Його входи відповідають булевим змінним, а вихід – значення функції. Графічні символи і назви найчастіше використовуваних логічних елементів зображено в таблиці1.

Набір логічних елементів повний, якщо з його допомогою можна реалізувати будь-яку булеву функцію. Логічна схема будується з набору базових елементів і зображує суперпозицію даних елементів так само, як формула є суперпозицією базових функцій булевої алгебри.

Логічні елементи, що реалізують операції з властивостями асоціативності, на схемах можуть зображуватися з числом входів більше двох, що означає багаторазове застосування даної операції.

Наприклад, логічний елемент АБО може мати 3 входи:

Приклад. Побудувати логічний ланцюг, що реалізує функцію f(x, y, z) = (x⋁y)∧z.

Але на практиці елементи, що реалізують логічні функції не існують в вигляді окремих вузлів, а входять до складу корпусу певної мікросхеми. На рисунку 1 наведені приклади умовного позначення логічних елементів різних серій.

2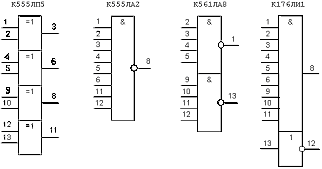

Рис.1а

3

Рис.1б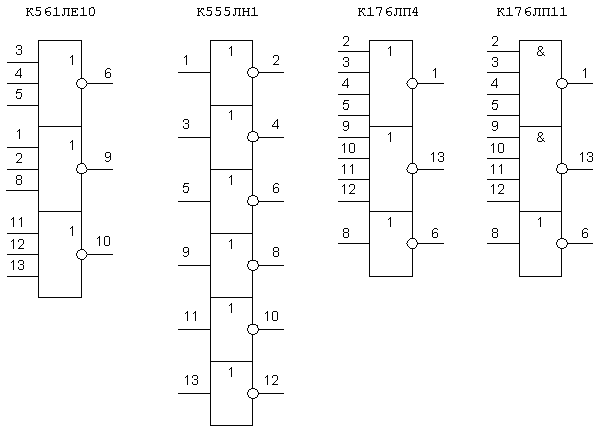

Мікросхеми, які виконують найпростіші операції (І, І-НІ, АБО, АБО-НІ та ін.), містять у своєму корпусі декілька незалежних логічних елементів (вентилів), пов’язаних тільки живленням. При складанні схеми дискретного пристрою трапляється, що окремі логічні елементи мікросхеми залишаються вільними. Це приводе до зайвих енергетичних затрат. Щоб цього по можливості уникнути треба намагатись певні фрагменти схеми будувати на одному базисі. Базис – це система логічних операцій, що реалізуються однією мікросхемою. Існують такі базиси:

Базис 1 утворює система функцій І, АБО, НЕ ( , , ). Він відноситься до збиткового, бо потребує використання кількох корпусів логічних елементів різних серій.

Базис 2 утворює система функцій І, НЕ( , ).

Б

2

азис 3 – АБО, НЕ( , ).

Базис 4 утворює функцію Шеррера І-НЕ ( ).

Базис 5 утворює функцію Пірса АБО-НЕ ( ).

Якщо базис 1 вважається збитковим, то базиси 4 і 5 – мінімальними.

Отже, для реалізації складних ЛФ, крім мінімізації функції треба намагатися витратити найменшу кількість корпусів логічних елементів. Для цього треба структурну формулу привести до такого вигляду, щоб вона містила тільки елементи І-НЕ або тільки АБО-НЕ. Тоді перехід від структурної формули до функціональної схеми не буде складним. В будь-якому випадку при побудові логічної схеми в базисі І-НЕ на основі логічної функції, поданої в МДНФ, необхідно скрізь замість елементів І і АБО вставити елементи І-НЕ. При побудові логічної схеми в базисі АБО-НЕ на основі МКНФ замість елементів І і АБО вставити елементи АБО-НЕ.

Н

4

а рисунку 2 приведені приклади універсальності вентилів І-НЕ і АБО-НЕ. Вони демонструють, як можливо дію будь-якої логічної функції подати через ці функції.

Рис. 2а. Властивість універсальності вентиля АБО-НЕ

4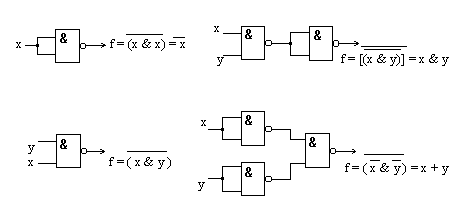

Рис.2б Властивість універсальності вентиля І-НЕ

AB CD	00	01	11	10
00	1	1	1	1
01	1	1	1	1
11
10	1		1

╔═···Приклад 1. Розглянемо приклад логічної функції F, визначеної таблицею істинності в вигляді карти Карно. По карті мінімізуємо функцію: МДНФ F= c̅+ a̅ b̅ d̅+ abd̅

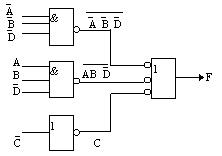
На рисунку приведена схема, що відповідає рівнянню. В приведеній схемі для елементів І і ІІ ступені застосовані операції І, АБО, НЕ.

5

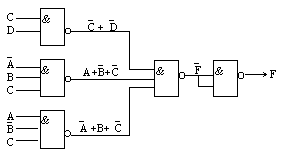
По приведеній карті Карно складемо мінімальну КНФ:

F = (C̅ +D̅)(A +B̅ +C̅)(A̅ + B +C̅). Приведемо її до базису І-НЕ:

╚═···

╔═···Приклад 2. Розглянемо функцію, функціональна схема якої приведена раніше в прикладі:

f(x, y, z) = (x⋁y)∧z =

1 2 3 4 5

Ф орма 1 – вихідна функція, 2 – подвійна інверсія вихідної функції, 3 – закон де Моргана дає функцію в базисі АБО-НЕ. Спробуємо використовуючи логічні перетворення привести логічну функцію в базис І-НЕ. Далі застосувавши ще закон де Моргана маємо форму 5 – функція в базисі І-НЕ.

╚═···