Перетворення чисел із шістнадцяткової системи у десяткову

Р 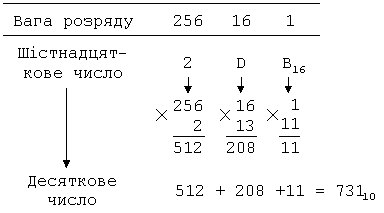озглянемо, як перетворити шістнадцяткове число 2DB₁₆ у його десятковий еквівалент. Ваги перших трьх розрядів шістнадцяткового числа рівні відповідно 256, 16 і 1.

У цьому шістнадцятковому числі є одиннадцять одиниць, в розряді з вагою 16 стоїть число 13, яке при множенні на вагу розряду дає число 208, а двійка в розряді з вагою 256 позначає число 512. Складаючи суму 11+208+512, знаходимо число 731₁₀. Таким чином, 2DB₁₆=731₁₀.

Переведення у десяткову систему числа x, записаного в q-тій системі числення (q = 2; 8 або 16) у виді:

x_q = (a_na_n-1 ... a₀ , a_-1 a_-2 ... a_-m)_q

зводиться до обчислення значення багаточлена

x₁₀ = a_n*qⁿ+ a_n-1*q^n-1 +...+a_0*q⁰ +a_-1*q ^-1 +a_-2*q^-2 +...+ a_-m*q^-m

засобами десяткової арифметики.

Перетворення чисел із десяткової системи в шістнадцяткову

Розглянемо тепер зворотне перетворення десяткового числа 47 в його шістнадцятковий еквівалент. Покажемо процедуру послідовних ділень на 16.

Перше ділення десяткового числа 47 на 16 дає частку 2 і остачу 15. Цю остачу (тобто число F в шістнадцятковій системі) слід взяти як останню вагому цифру шуканого шістнадцяткового числа. Частку (у даному випадку 2) потрібно прийняти далі як ділиме і знову розділити його на 16. У результаті получиться частка 0 з остачею 2 ; цю цифру потрібно вважати наступною цифрою шуканого шістнадцяткового числа. На цьому процес перетворення закінчується, оскільки получилась частка, рівна 0. Запишемо результат: 47₁₀=2F₁₆.

Переведення цілого числа з десяткової системи у будь-яку іншу систему числення.

Ä Для переведення цілого десяткового числа N у систему числення з основою q необхідно N розділити з залишком ("нацело") на q , записане в тій же десятковій системі. Потім неповну частка, отриману від такого ділення, потрібно знову розділити з залишком на q , і т.д., поки остання отримана неповна частка не стане рівною нулю. Представленням числа N у новій системі числення буде послідовність залишків від ділення, зображених однією q-тою цифрою і записаних у порядку, зворотному порядку їх одержання.

╔═··· Приклад 1. Переведемо число 75 з десяткової системи у двійкову, вісімкову та шістнадцяткову.