Переведення чисел з десяткової системи числення в двійкову

Для переведення чисел із системи числення з основою p в систему числення з основою q з використанням арифметики старої системи числення з основою p потрібно:

• для переведення цілої частини:

послідовно кожен результат (спочатку це саме число), записане в системі основою p ділити на основу нової системи числення, виділяючи остачі. Останні записані у зворотному порядку, будуть утворювати число в новій системі числення;

• для переведення дробової частини:

послідовно дробову частину множити на основу нової системи числення, виділяючи цілі частини, які й будуть утворювати запис дробової частини числа в новій системі числення.

Цим самим правилом зручно користуватися в разі переведення з десяткової системи числення, тому що її арифметика для нас звичніша.

╔═··· Приклад 5. Визначити десяткове значення числа, поданого в двійковій системі числення 999,35₁₀

Розв’язування.

для цілої частини:

для дробової частини:

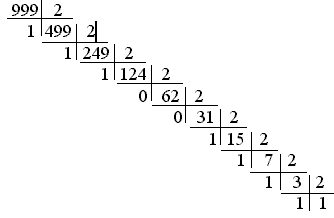
999,3510=1111100111,010112 ╚═···

Для самостійної роботи

Критерії оцінювання:

1-5бали – конспект приведених прикладів;

Кожний розв’язаний приклад – 3 бали.

Максимальна кількість балів – 12.

Завдання 1. Визначити десяткове значення числа, поданого в двійковій системі числення.

Завдання 2. Визначити двійкове значення числа, поданого в десятковій системі числення.

Завдання 3. Визначити двійкове значення числа, поданого в десятковій системі числення.

Завдання 4 Визначити двійкове значення числа, поданого в десятковій системі числення.

Варіант	Завдання 1	Завдання 2	Завдання 3	Завдання 4
1	101101,0101	595	0,622	22,90
2	111010,0011	472	0,502	18,82
3	101101,1001	628	0,482	25,79
4	101011,1101	597	0,695	9,69
5	100101,1011	950	0,528	16,85
6	101110,0111	683	0,399	30,73

Самостійна робота № 3

Тема: Переведення чисел з використанням вісімкової та шістнадцяткової системи числення.

Мета: Закріпити набуті знання та навички, перевірити їх при виконанні практичних завдань.

Завдання

1. Засвоїти теоретичний матеріал згідно теми;

2. Дати відповіді на поставлені питання (лекція 4);

3. Виконати письмово приведені завдання;

4. Випишіть питання, що виникли в ході засвоєння матеріалу;

5. Зробіть висновки.

Рекомендована література:

1. Стрыгин В.В., Щарев Л.С. Основы вычислительной микропроцессорной техники и программирования: Учеб. для вузов. – М.: Высш. Шк., 1989. – 479с.

2. В.В. Коштоев, К.К. Кипиани „Основы прикладной теории_цифровых автоматов” Т: Учебное пособие. – Тбилиси:1998. – 155 с.(електронний посібник)