Подання чисел в еом із плаваючою комою
При використанні чисел з плаваючою комою у розрядну сітку машини записується не тільки саме число в деякому масштабі, але і сам масштаб цього числа. У напівлогарифмічній формі подання будь-яке число x має вигляд: x=SP·M, де S – основа системи числення, Р – ціле число, що називають порядком, М-мантиса числа, | M | <1.
У розрядну сітку числа звичайно записується не сама степінь основи SP, а тільки порядок P і мантиса числа M. Наприклад, число у = 24.12 у напівлогарифмічній формі в звичайній десятковій системі числення буде мати вид: у = 102 0,2412 або y = 103 0,02412 і т.п.
Як правило, число в форматі з плаваючою комою повинно бути нормалізоване, тобто мантиса повинна знаходитись в діапазоні 0,1≤|M|<1. Наприклад, число 103·0,02412 не нормалізоване, в мантисі після коми повинно бути будь-яка цифра, тільки не 0. Нормалізація: 103·0,02412 = 102·0,2412 – при перенесенні коми в мантисі вліво – порядок зменшується на 1, вправо - збільшується.
Оскільки масштаб числа при його записі в напівлогарифмічній формі записується в розрядну сітку машини, то операції запам'ятовування, вирівнювання масштабів (порядків) і т.п. виконуються машиною і не потребують особистої участі з боку людини. Правда, після виконання операцій може потребуватися нормалізація мантиси і відповідна зміна порядку. Але ці операції досить просто реалізуються в машині.
При виконанні операцій над числами, поданими у формі з плаваючою комою, можливо одержання результату, порядок котрого більше припустимого в машині. Це також варто враховувати при проведенні обчислень. Наприклад, нехай потрібно обчислити z = wv/u, причому w = 1010 0,4, v = 108 0,3 і u = 108 0,2, а максимально припустимий порядок у машині 1012. Якщо спочатку підрахувати множення wv, то відбудеться так зване переповнення один по одному і машина припинить обчислення. Якщо ж спочатку виконати операцію ділення у = w/u, а потім множення yv, одержимо потрібний результат.
При поданні чисел у напівлогарифмічній формі також виникає проблема кодування знака. Вона вирішується так само, як і для поданні чисел у формі з фіксованою комою, але додаткових розрядів потрібно вже два – для знака порядку і знака мантиси.
Р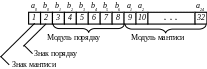
озглянемо
як приклад розрядну сітку для представлення
двійкових чисел у 32 розрядах .
Розрядна сітка машини з плаваючою комою (з урахуванням розрядів під знаки мантиси і порядку)
Нехай
запис числа має вигляд:
.
Перші два розряди виділяються під знаки
мантиси (числа) і порядку відповідно,
розряди з 3-го по 8-й виділяються під
запис модуля порядку, а 24 розряди з 9-го
по 32-й – під запис модуля мантиси. Тоді
діапазон подання чисел буде визначатися
в такий спосіб:
,
що приблизно відповідає діапазону
чисел від 10-19
до 1019.
Як уже відзначалося, форма подання з плаваючою комою є основною формою подання чисел у сучасних обчислювальних машинах. До її недоліків відносять зменшення продуктивності машини в порівнянні з обчисленнями в природній формі, ускладнення її технічних пристроїв. Наприклад, повинні бути розроблені схеми нормалізації, передбачене устаткування для виконання операцій над порядками і мантисами чисел і т.п. Обчислювальні машини, у яких може бути використана і та й інша форми подання, дозволяють врахувати особливості розв'язуваної задачі і підвищити продуктивність обчислень.
╔═··· Приклад 1. Число х=222,24 подати в комп’ютерній формі подання в форматі з фіксованою точкою. Для зображення чисел в уявній ЕОМ використовувати двобайтне слово. Який при цьому може бути масштаб числа, щоб точність числа була найбільшою?
Переведемо число в 2-ву СЧ: х=222,24=11011110,001111012.
Слово довжиною в 2 байти містить 16 розрядів для зображення числа, причому крайній лівий 0-й розряд відводиться під знак. Отже для зображення числа відведено 15 розрядів, з 1-го по 15-й.
Для числа x повинен бути введений відповідний масштаб Mx, так що добуток Mxx потрапив в прийнятий діапазон зображення чисел, тобто, щоб |Mxx|<1 треба перенести кому в числі х на 10 розрядів вліво, тобто помножити на 2-10. Одже Mx=2-10.
№ розрядів |
1 |
2 |
3 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Код числа |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
╚═···
╔═··· Приклад 2. Число х=222,24 подати в комп’ютерній формі подання в форматі з плаваючою точкою. Для зображення чисел в уявній ЕОМ використовувати слово в 4 байти за приведеним зразком.
Переведемо число в 2-ву СЧ: х=222,24=11011110,001111012
Нормалізуємо число: х=11011110,001111012 =0,1101111000111101·1010.
Порядок р=10=10102, мантиса m=1101111000111101, знаки числа і порядку +, тобто кодуються 0.
№ розрядів |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
. . . . |
27 |
28 |
29 |
30 |
31 |
Код числа |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
. . . . |
0 |
0 |
0 |
0 |
0 |
З |
|
|
п |
м |
|||||||||||||||||
Знак порядку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
нак
числа
орядок
антиса╚═···
Самостійна робота № 7
Тема: Арифметичні операції в кодах ЕОМ.
Мета: Закріпити набуті знання та навички, перевірити їх при виконанні практичних завдань.
Завдання
Засвоїти теоретичний матеріал згідно теми;
Дати відповіді на поставлені питання (лекція 11);
Виконати письмово приведені завдання;
Випишіть питання, що виникли в ході засвоєння матеріалу;
Зробіть висновки.
Рекомендована література:
Стрыгин В.В., Щарев Л.С. Основы вычислительной микропроцессорной техники и программирования: Учеб. для вузов. – М.: Высш. Шк., 1989. – 479с.
В.В. Коштоев, К.К. Кипиани „Основы прикладной теории_цифровых автоматов” Т: Учебное пособие. – Тбилиси:1998. – 155 с.(електронний посібник)
Нагадаємо операцію додавання (віднімання) цілих чисел.
╔═··· Приклад 1. Знайти модифіковані коди чисел x=-77, y=-55, а також їх суму.
x=-77=-10011012; y=-55=-1101112.
-
х – прямий код,
1
1
0
0
0
0
0
0
0
1
0
0
1
1
0
1
зворотний,
1
1
1
1
1
1
1
1
1
0
1
1
0
0
1
0
додатковий
1
1
1
1
1
1
1
1
1
0
1
1
0
0
1
1
-
у – прямий код,
1
1
0
0
0
0
0
0
0
0
1
1
0
1
1
1
зворотний,
1
1
1
1
1
1
1
1
1
1
0
0
1
0
0
0
додатковий
1
1
1
1
1
1
1
1
1
1
0
0
1
0
0
1
Щоб знайти суму х і у додамо додатковий код числа х і додатковий у:
-
-77-55
1
1
1
1
1
1
1
1
0
1
1
1
1
1
0
0
Одиниця, що вийшла за межі розрядної сітки ігнорується. Код знака свідчить про те, що результат – від’ємне число, отже воно подане в додатковому модифікованому коді. Переведемо результат в десяткове число:
-
х+у – додатковий
1
1
1
1
1
1
1
1
0
1
1
1
1
1
0
0
зворотний,
1
1
1
1
1
1
1
1
0
1
1
1
1
0
1
1
прямий
1
1
0
0
0
0
0
0
1
0
0
0
0
1
0
0
х+у = -100001002=-(128+4)=-132.
Перевірка: -77-55=-132.
╚═···
Для дійсних чисел з фіксованою комою процедура додавання мало відрізняється від додавання цілих. Адже і в математиці, записуємо додатні розряд під відповідним розрядом, додаємо числа не звертаючи увагу на кому, а потім в результат зносимо кому. Але в комірках пам’яті ЕОМ уявна кома вже присутня.
Нагадаємо форму подання дійсних чисел в ЕОМ з фіксованою комою:
Вага розряду |
2k |
|
. . . . . |
21 |
20 |
2-1 |
. . . . . . |
|
2k-n |
Код числа |
a0 |
a1 |
. . . . . |
ak-1 |
ak |
ak+1 |
. . . . . . |
|
an |
№ розряду |
0 |
1 |
. . . . . |
k-1 |
k |
k+1 |
. . . . . . |
n-1 |
n |
Рисунок 1 - Розрядна сітка машини з поданням чисел з фіксованою комою
╔═··· Приклад 2. Знайти коди чисел x=77,33 і y=-55,12 в форматі з фіксованою комою. Знайти суму в кодах ЕОМ. Визначимо для уявної ЕОМ фомат числа в 2-х байтах (16 розрядів – з 0-го по 15-й), що розподіляються таким чином: 0-й – знак числа, з 1-го по 8-й розряди – ціла частина числа, з 9-го по 15-й – дробна частина.
x=77,33 =1001101,010010002; y=-55,12 =-110111,0000111012.
-
х – прямий код,
0
0
1
0
0
1
1
0
1
0
1
0
0
1
0
0
-
у – прямий код,
1
0
0
1
1
0
1
1
1
0
0
0
0
1
1
1
зворотний,
1
1
1
0
0
1
0
0
0
1
1
1
1
0
0
0
додатковий
1
1
1
0
0
1
0
0
0
1
1
1
1
0
0
1
Щоб знайти суму х і у додамо додатковий код числа х і додатковий у:
-
77,33 -55,12
0
0
0
0
1
0
1
1
0
0
0
1
0
1
0
1
Одиниця, що вийшла за межі розрядної сітки ігнорується. Код знака свідчить про те, що результат – додатне число, отже воно подане в прямому коді. Переведемо результат в десяткове число:
х+у = 10110,01100112=22,164.
Перевірка: 77,33 -55,12=22,21 – неспівпадіння в дробній частині за рахунок того, що дробна частина не вмістилася в розрядній сітці.
╚═···
Як виконуються дії в ЕОМ з нормалізованими числами? Нагадаємо форму подання чисел з плаваючою комою: число х=222,24 в форматі з плаваючою точкою:
№ розрядів |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
. . . . |
27 |
28 |
29 |
30 |
31 |
Код числа |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
. . . . |
0 |
0 |
0 |
0 |
0 |
З нак числа |
|
|
п орядок |
м антиса |
|||||||||||||||||
Знак порядку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
До початку операції додавання, віднімання виконується підготовча дія – вирівнювання порядків. В процесі вирівнювання порядків мантиса числа з меншим порядком здвигається вправо на кількість розрядів, рівне різниці порядків операндів. Після кожного здвигу значення порядку збільшується на одиницю. Після вирівнювання порядків додаються тільки мантиси. Розглянемо процедуру в десятковій системі числення:
╔═··· Приклад 3. х = 0,244·104; у = 0,135·102 ; х + у = ?
у = 0,135·102 = 0,0135·103 = 0,00135·104 – вирівнюємо порядки;
х + у = 0,244·104 + 0,00135·104 = 0,24535·104.
╚═···
В випадку необхідності результат нормалізується шляхом здвигу мантиси вліво, при цьому порядок зменшується на 1.
╔═··· Приклад 4. Додати двійкові нормалізовані числа 0.10111·10–1 і 0.11011·1010.
Різниця порядків дорівнює 3-м, тому перед додаванням вирівнюємо порядки:
0.10111·10–1 = 0.00010111·1010;
0.00010111·1010 + 0.11011·1010 = 0.00010111·1010 0000101000010111
0.11011000·1010 0000101011001000
╚═··· 0.11101111·1010 0000101011101111
╔═··· Приклад 5. Виконати віднімання двійкових нормалізованих чисел 0.10101·1010 і 0.11101·101.
Різниця порядків дорівнює 1, тому перед додаванням вирівнюємо порядки:
0.11101·101= 0.011101·1010;
0.10101·1010 - 0.011101·1010= 0.101010·1010 0000101010101000
0.011101·1010 0000101001110100
0.001101·1010 0000101000110100
Отриманий результат не нормалізований, тому після нормалізації 0.001101·1010= 0.1101·100.
╚═···