21 Вопрос

Электрический ток в полупроводниках

По значению удельного электрического сопротивления полупроводники занимают промежуточное положение между хорошими проводниками и диэлектриками. К числу полупроводников относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк и др.) Качественное отличие полупроводников от металлов проявляется прежде всего в зависимости удельного сопротивления от температуры. С понижением температуры сопротивление металлов падает  У полупроводников, напротив, с понижением температуры сопротивление возрастает и вблизи абсолютного нуля они практически становятся изоляторами Необходимым условием резкого уменьшения удельного сопротивления полупроводника при введении примесей является отличие валентности атомов примеси от валентности основных атомов кристалла.

Электронная проводимость возникает, когда в кристалл германия с четырехвалентными атомами введены пятивалентные атомы Дырочная проводимость возникает, когда в кристалл германия введены трехвалентные атомы Следует подчеркнуть, что дырочная проводимость в действительности обусловлена эстафетным перемещением по вакансиям от одного атома германия к другому электронов, которые осуществляют ковалентную связь.

Для полупроводников n- и p-типов закон Ома выполняется в определенных интервалах сил тока и напряжений при условии постоянства концентраций свободных носителей.

22 Ток в газах Явление протекания электрического тока через газ, наблюдаемое только при условии какого-либо внешнего воздействия на газ, называется несамостоятельным электрическим разрядом. Процесс отрыва электрона от атома называется ионизацией атома. Минимальная энергия, которую необходимо затратить для отрыва электрона от атома, называется энергией ионизации. Частично или полностью ионизированный газ, в котором плотности положительных и отрицательных зарядов одинаковы, называется плазмой. В сильно неоднородных электрических полях, образующихся, например, между острием и плоскостью или между проводом линии электропередачи и поверхностью Земли, возникает особая форма самостоятельного разряда в газах, называемая коронным разрядом. Разряд, возникающий при пониженном давлении, называется тлеющим разрядом.

Несамостоятельный и самостоятельный газовый разряд. Известно, что в обычном состоянии газовый промежуток является хорошим изолятором Самостоятельные разряды характеризуются тем, что заряженные частицы, необходимые для поддержания разряда, создаются в процессе самого разряда, то есть их количество по крайней мере не уменьшается с течением времени Несамостоятельный разряд – возможен только при наличии «искусственного» эмиттирования электронов из катода 

23 Понятие о плазме  — частично или полностью ионизированный газ, образованный из нейтральных атомов и заряженных частиц.  Важнейшей особенностью плазмы является ее квазинейтральность, это означает, что объемные плотности положительных и отрицательных заряженных частиц, из которых она образована, оказываются почти одинаковыми. Плазма иногда называется четвёртым агрегатным состоянием вещества.

Пла́зменная частота́ — частота собственных продольных колебаний пространственного заряда в однородной плазме в отсутствие магнитного поля. В пренебрежении движением ионов плазменная частота электронного газа равна

Дебаевская длина — расстояние, на которое распространяется действие электрического поля отдельного заряда в нейтральной среде, состоящей из положительно и отрицательно заряженных частиц. Дебаевская длина определяется формулой Электропроводность плазмы может быть очень большой и по характеру приближается к электронной электропроводности металлов. Плазма имеется в положительном столбе тлеющего разряда и в главном канале искрового разряда. Электропроводность плазмы  определяется ее температурой которая, в свою очередь, зависит от удельной мощности Р, выделяющейся в плазме

\

24 Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения магнитная составляющая электромагнитного поля. Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах. Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции   . С математической точки зрения   — векторное поле,

Ещё одной фундаментальной характеристикой магнитного поля является векторный потенциал.

Магни́тная инду́кция   — векторная величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Определяет, с какой силой   магнитное поле действует на заряд  , движущийся со скоростью  .

Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постояннымэлектрическим током и вектор

25 Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постояннымэлектрическим током и вектор

Аналогично электрическому, для магнитного поля выполняется принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:  Применим закон Био-Савара-Лапласа для расчета магнитных полей простейших токов.

Д ля бесконечно длинного проводника α1 = 0, а α2 = π и следовательно:

М агнитное поле кругового тока поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности радиуса R

26 Магнитное поле движущегося заряда в нерелятивистской форме. Взаимодействие точечных неподвижных зарядов полностью описывается законом Кулона. Однако закона Кулона недостаточно для анализа взаимодействия движущихся зарядов. Такой вывод следует не из конкретных особенностей кулоновского взаимодействия, а обусловливается релятивистскими свойствами пространства и времени, релятивистскими уравнениями движения.

      Релятивистское уравнение движения имеет одинаковый вид во всех инерциальных системах отсчёта: Требования релятивистской инвариантности уравнения движения приводит к тому, что силы оказываются связанными определенными соотношениями при переходе от одной ИСО к другой. Причём из формулы преобразования сил следует неизбежная зависимость силы от скорости в релятивистской теории.

      Существование магнитной и электрической сил можно выявить из следующего примера взаимодействия зарядов.

27 Вихревой характер магнитного поля

Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей. Мы видим, что магнитное поле есть вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического.

28 Зако́н Ампе́ра  — закон взаимодействия электрических токов.  Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы  , с которой магнитное поле действует на элемент объёма   проводника с током плотности  , находящегося в магнитном поле с индукцией  Если ток течёт по тонкому проводнику, то 

Модуль силы Ампера можно найти по формуле:

Закон Ампера. Сила, действующая между проводниками. В соответствии с законом Био — Савара — Лапласа бесконечный проводник с током   в точке на расстоянии   создаёт магнитное поле с индукцией

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

Таким образом, из полученной формулы и определения ампера следует, что магнитная постоянная   равна   Н/А² или, что то же самое,   Гн/ м точно.

29 Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Выражается в СИ как: Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом E и магнитном Bполях, такова:

Непрерывное распределение заряда

Для непрерывного распределения заряда, сила Лоренца принимает вид:

Движение заряженных частиц в магнитном поле

Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях. Период вращения частицы    (период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<<c)

30 Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов при помещении проводника с постоянным током в магнитное поле Аномальный эффект Холла Случай появления напряжения  в образце, перпендикулярного направлению пропускаемого через образец тока наблюдающегося в отсутствие приложенного постоянного магнитного поля Квантовый эффект Холла В сильных магнитных полях в плоском проводнике в системе начинают сказываться квантовые эффекты, что приводит к появлению квантового эффекта Холла

Применение

Эффект Холла, в некоторых случаях, позволяет определить тип носителей заряда в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников. На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля.

31 Момент сил и работа при перемещении контура с током в магнитном поле. Рассмотрим постоянное магнитное поле. Работа сил Ампера при элементарном перемещении ,

где   - приращение магнитного потока. При перемещении контура с током из начального положения 1 в конечное 2   и при  :  .

Магнитный момент витка с током это физическая величина, как и любой  другой магнитный момент, характеризует магнитные свойства данной системы. Величину магнитного момента кругового витка с током можно определить по формуле.

32 Магни́тный пото́к — поток   как интеграл вектора магнитной индукции   через конечную поверхность  . Определяется через интеграл по поверхности при этом векторный элемент площади поверхности определяется как , Магнитный поток через контур также можно выразить через  циркуляцию векторного потенциала магнитного поля по этому контуру: Теорема Гаусса для магнитной индукции В соответствии с теоремой Гаусса для магнитной индукции поток вектора магнитной индукции через любую замкнутую поверхность равен нулю: Или, в дифференциальной форме — дивергенция магнитного поля равна нулю:

Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:

33 Явление электромагнитной индукции очень широко используется в электротехнике. На явлении индукции основано устройство всех электрических машин Электромагнитная индукция — - возникновение электрического тока в замкнутом проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле так, что число линий магнитной индукции, пронизывающих контур, меняется. Чем быстрее меняется число линий магнитной индукции, тем больше индукционный ток. Правило Ленца

Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует изменению магнитного потока, которым он вызван.

Применение правила Ленца 1. показать направление вектора В внешнего магнитного поля;  2. определить увеличивается или уменьшается магнитный поток через контур; 

3. показать направление вектора Вi магнитного поля индукционного тока 4. по правилу буравчика определить направление индукционного тока в контуре.

Закон электромагнитной индукции в интегральной и дифференциальной формах.

Согласно закону электромагнитной индукции Фарадея (в СИ):

В дифференциальной форме закон Фарадея можно записать в следующем виде:

 

34 Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре ^[1]при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Это явление и называется самоиндукцией.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока I,

.

Коэффициент пропорциональности L называется коэффициентом самоиндукции или индуктивностью контура Индукти́вность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность^[1], краем которой является этот контур.^[2][3][4].

В формуле

Релаксация — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.

35 Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре ^[1]при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Это явление и называется самоиндукцией.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока I,

.

Коэффициент пропорциональности L называется коэффициентом самоиндукции или индуктивностью контура Индукти́вность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность^[1], краем которой является этот контур.^[2][3][4].

В формуле

Релаксация — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.

36 Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции.

 Явление взаимоиндукции широко используется для передачи энергии из одной электрической цепи в другую, для преобразования напряжения с помощью трансформатора. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи) встречает противодействие со стороны другой цепи 

ВЗАИМНАЯ ИНДУКТИВНОСТЬ, коэффициент взаимной индуктивности – величина, характеризующая отношение потокосцепления одной цепи (катушки) к току другой цепи (катушки), возбуждающему это потокосцепление. В Международной системе единиц (СИ) измеряется в генри

37 Энергия магнитного поля. Объемная плотность энергии магнитного поля.

Энергия магнитного поля

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.

Энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, равна  W_м = LI²/ 2

Объемная плотность энергии пропорциональна квадрату напряженности поля. Объемная плотность энергии, магнитного - поля, прямо пропорциональна квадрату напряжен-ности магнитного поля в данном месте пространства Объемная плотность энергии в данной точке любого поля тоже равна этому выражению. Размерность объемной плотности энергии совпадает с размерностью давления

38 Магнитное поле в веществе  индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме. Физическая величина, показывающая, во сколько раз индукция B магнитного поля в однородной среде отличается по модулю от индукции  B0 магнитного поля в вакууме, называется магнитной проницаемостью: 

Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым

Магнитные моменты атомов  Различные среды при рассмотрении их магнитных свойств называют магнетиками. Если магнитное поле слабо усиливается в веществе, то такое вещество называется парамагнетиком: если ослабевает, то это диамагнетик:

Виды магнитных материалов

Магнитотвёрдые материалы:

Магнитомягкие материалы:

Магнитострикционные материалы:

Магнитооптические материалы:

Термомагнитные материалы:

Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычноМ или J. Определяется как магнитный момент единицы объёма вещества:

Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом вещества и магнитным полем в этом веществе

39 ферромагнетик — такое вещество, которое, при температуре ниже точки Кюри, способно обладать намагниченностью в отсутствие внешнего магнитного поля

Кривая намагничивания ависимости B=F(H) и J=F(H), полученные на предварительно размагниченных образцах, называют основными кривыми намагничивания.

Основная кривая намагничивания — важнейшая характеристика магнитных материалов. Физика процессов намагничивания магнитных материалов может быть понята при отождествлении ее с характерными участками основной кривой намагничивания. 

Гистере́зис свойство систем мгновенный отклик которых на приложенные к ним воздействия Домен — макроскопическая область в магнитном кристалле, в которой ориентация вектора спонтанной однородной намагниченности иливектора антиферромагнетизма.

спиновая природа ферромагнетизма заключается в разряжении нейрона, подлетающего слишком близко аноду. В результате ядро молекулы расщепляется и распадается на энергию. Такой метод еще называется спинным.

40 Закон полного тока для магнитного поля в веществе 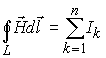Выражение представляет собой теорему о циркуляции вектора   или закон полного тока и гласит: Циркуляция вектора напряженности магнитного поля   по любому замкнутому контуру Lравна алгебраической сумме макротоков, охватываемых контуром. Вектора напряженности магнитного поля   являясь аналогом электрического смещения  ,определяется только макротоками.

 Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B ивектора намагниченности M.

В СИ:  В вакууме напряжённость магнитного поля совпадает с вектором магнитной индукции с точностью до коэффициента, равного μ₀ в СИ. Магнитная проницаемость — физическая величина, коэффициент характеризующий связь между магнитной индукцией   и напряжённостью магнитного поля   в веществе. Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды

В общем связь соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как

41 Вихревое электрическое поле это индуцированное электрическое поле. Переменное магнитное поле порождает наведенное (индуцированное) электрическое поле. Если магнитное поле постоянно, то индуцированного электрического поля не возникает. Следовательно, индуцированное электрическое поле не связано с зарядами, как в случае электростатического поля; его силовые линии не начинаются и не заканчиваются на зарядах, а замкнуты сами на себя, подобно силовым линиям магнитного поля

Ток смещения или абсорбционный ток — величина, прямо пропорциональная быстроте изменения электрической индукции. Это понятие используется в классической электродинамике. Строго говоря, ток смещения не является^[2] электрическим током, но измеряется в тех же единицах, что и электрический ток. В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения   (с точностью до универсального постоянного коэффициента) называется^[3] поток вектора быстроты изменения электрического поля   через некоторую поверхность^[4]  :

42  Максвелла уравнения позволяют определить основные характеристики поля (Е, В, D и Н) в каждой точке пространства в любой момент времени, если известны источники поля j и r как функции координат и времени.Максвелла уравнения могут быть записаны в интегральной или в дифференциальной форме  Первое Максвелла уравнения имеет вид:  Первое Максвелла уравнения является обобщением на переменные поля эмпирического Ампера закона о возбуждении магнитного поля электрическими токами.  Второе Максвелла уравнения является математической формулировкой закона электромагнитной индукции Фарадея  Третье Максвелла уравнения выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим Четвёртое Максвелла уравнения (обычно называемое Гаусса теоремой) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов — Кулона закона:

Свойства   1. Система уравнений Максвелла "замкнута", то есть число неизвестных функций равно числу уравнений в системе.

     2. Система уравнений Максвелла "конструктивна". В математическом анализе доказано, что одновременное задание ротора и дивергенции векторного поля позволяет это поле рассчитать (при выполнении определенных граничных условий). Уравнения (7.1)- (7.4) как раз и задают роторы и дивергенции электрического и магнитного полей, причем ротор электрического поля связан со скоростью изменения магнитного поля, а ротор магнитного поля - со скоростью изменения электрического поля.

     3. Система уравнений Максвелла обладает свойством инвариантности относительно преобразований Лоренца (основа современной теории относительности). Классическая механика Ньютона этим свойством не обладает.

     4. Система уравнений Максвелла удивительно "симметрична" относительно электрических и магнитных величин. Это свойство особенно наглядно проявляется в непроводящей среде в отсутствие объемной плотности свободных электрических зарядов.

43 Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока. Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

Резонансная частота контура определяется так называемой формулой Томсона:

 При отсутствии активного сопротивления амплитуда колебаний остается неизменной. Такие колебания называются незатухающим В действительности колебательный контур имеет некоторое активное сопротивление; оно распределено главным образом в катушке, а также в соединительных проводах и отчасти в конденсаторе.

44 затухающие колебания – колебания, у которых амплитуды из-за потерь энергии колебательной системой с течением времени убывают Дифференциальное уравнение свободных затухающих колебаний линейной системы определяется как   Решение уравнения запишем в виде     u=u(t)  

  амплитуда затухающих колебаний. Промежуток времени τ = 1/σ, в течение которого амплитуда затухающих колебаний становится мешьше в е раз, называется временем релаксации. Период     называется декрементом затухания

45 Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодическое воздействие. Рассмотрим этот вопрос кратко, используя аналогию с механическими колебаниями.

Это уравнение вынужденных электрических колебаний. ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: ,где r и x активное и реактивное сопротивления.

Мощность в цепи постоянного ток

P=UI

мощность в цепи переменного тока

Активная мощность - количество электрической энергии, преобразованной в тепло. Для цепей переменного тока, когда ток и напряжение изменяются по синусоидальному закону с одинаковой частотой, она равна:

P=UIcosφ

Реактивная мощность цепи переменного тока характеризует скорость накопления энергии в конденсаторах и катушках индуктивности, а также обмен энергией между отдельными участками цепи, и в частости, генератором и приемником.

P=UIsinφ

Действующее значение переменного тока. Иначе говоря, действующее значение тока можно определить по формуле: .

Для гармонических колебаний тока

Аналогичным образом определяются действующие значения ЭДС и напряжения.

46 Дифференциальное уравнение электромагнитной волны Одним из важнейших следствий уравнений Максвелла является существование электромагнитных воли. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа

В вакууме (при e=1 и m=l) скорость распространения электромагнитных волн совпадает со скоростью с. Так как em > 1, то скорость распространения электромагнит­ных воли в веществе всегда меньше, чем в вакууме. Основными свойствами электромагнитных волн являются:

1)поглощение;2)рассеяние;

3)преломление;4)отражение;

5)интерференция;6)дифракция;

7)поляризация.

Монохроматическая волна — модель в физике, удобная для теоретического описания явлений волновой природы, означающая, что в спектр волны входит всего одна составляющая по частоте. Монохроматическая волна — строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой. Стоячая монохроматическая волна — волна, формирующаяся при распространении двух плоских монохроматических электромагнитных волн одинаковой поляризации навстречу друг другу.

47 Энергия электромагнитных волн Объёмная плотность энергии электромагнитного поля в линейной изотропной среде, как известно из электродинамики, даётся выражением. Вектор плотности потока энергии электромагнитной волны (то, что в теории упругих волн называется вектором Умова) называется вектором Умова-Пойнтинга, или чаще просто вектором Пойнтинга Р:    Модуль среднего значения вектора Пойнтинга называется интенсивностью электромагнитной волны:     Следует обратить внимание, что интенсивность электромагнитной волны зависит от амплитуды (либо электрического, либо магнитного поля; они связаны), но не зависит от частоты волны - в отличие от интенсивности упругих механических волн.

Пото́к эне́ргии — это количество энергии, переносимое через некоторую произвольную площадку в единицу времени. Если речь идёт об энергии, переносимой оптическим излучением, то вместо термина «поток энергии» используют эквивалентный для такого случая термин «поток излучения».(ватт) Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компоненттензора энергии-импульса электромагнитного поля. В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усреднённой по периоду комплексной плотности потока энергии В силу симметричности тензора энергии-импульса, все три компоненты вектора пространственной плотности импульса электромагнитного поля равны соответствующим компонентам вектора Пойнтинга, делённым на квадрат скорости света: