6 Вопрос

Электростатическая теорема Остроградского-Гаусса.Поток вектора   через.любую замкнутую.поверхность пропорционален.суммарному заряду, расположенному внутри этой поверхности.

Возможны три случая обращения в нуль потока вектора напряженности через замкнутую поверхность:

а) алгебраическая.сумма зарядов.внутри.поверхности равна нулю,  ;

б) зарядов.внутри.поверхности нет, но есть поле, связанное с внешними зарядами,  ;

в) нет ни поля, ни внутренних зарядов. Заряды могут быть распределены различным образом, причем они могут вноситься в рассматриваемое пространство, перемещаться в нем и изыматься из него, поэтому их называют свободными зарядами.

6

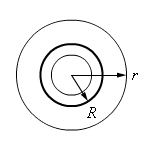
Рис. 2.

напряженность поля заряженной проводящей сферы радиуса R. Сфера заряжена по поверхности.

Внутри сферы заряда нет:

E = 0.
Снаружи сферы:

На поверхности сферы:

7 Вопрос

Электростатическая теорема Остроградского-Гаусса.Поток вектора   через.любую замкнутую.поверхность пропорционален.суммарному заряду, расположенному внутри этой поверхности.

Возможны три случая обращения в нуль потока вектора напряженности через замкнутую поверхность:

а) алгебраическая.сумма зарядов.внутри.поверхности равна нулю,  ;

б) зарядов.внутри.поверхности нет, но есть поле, связанное с внешними зарядами,  ;

в) нет ни поля, ни внутренних зарядов. Заряды могут быть распределены различным образом, причем они могут вноситься в рассматриваемое пространство, перемещаться в нем и изыматься из него, поэтому их называют свободными зарядами.

7 Метод коаксиальных цилиндров для определения коэффициента теплопроводности жидкостей жидкость заполняет кольцевой зазор между двумя коаксиально расположенными цилиндрами и радиальный тепловой поток проходит от внутреннего цилиндра, в полости которого находится основной нагреватель, через слой исследуемой жидкости к внешнему цилиндру. При наступлении стационарного состояния коэффициент теплопроводности жидкости определяется по перепаду температуры. Метод коаксиальных цилиндров может быть осуществлен как в стационарном, так и нестационарном варианте.

8 Вопрос

интегральная форма теоремы Гаусса характеризует соотношения между источниками электрического поля и характеристиками электрического поля Пусть в объеме   имеется

,

где  - средняя по объему плотность. Тогда

.

При стягивании объема в точку

.

 - теорема Гаусса в дифференциальной форме

или

 .

Здесь

- оператор Гамильтона (набла) (ранее встречался при рассмотрении  );

 - скалярное произведение   на   (обозначается точкой между множителями в отличие от  ).

В дифференциальной форме теорема Гаусса локальна: дивергенция вектора напряженности зависит от плотности   в данной точке (это еще одно свойство поля).

Дивергенция вектора напряженности во всех точках, где   (нет заряда), равна нулю

,

а там, где она не равна нулю, находятся стоки или источники поля