10.Поверхности второго порядка.

Эллипсоид : x^2/a^2 +y^2\b^2 +z^2/c^2 =1

Гиперболоид: x^2/a^2 +y^2\b^2 -z^2/c^2 =1 -однополостный гиперб.

x^2/a^2 +y^2\b^2 -z^2/c^2 =-1-двухполосный гиперб.

Парабалоид: 2z=x^2/p + y^2/q-эллиптический парабал.

2z=x^2/p - y^2/q -гиперболический парабал.

Цилиндр: x^2/a^2 +y^2\b^2 =1 - элмптический цилиндр

x^2/a^2 -y^2\b^2 =1 -гиперболический цилиндр

y^2 = 2px-параболический цилинд.

Конус: x^2/a^2 +y^2\b^2 -z^2/c^2 =0

11.Приведение общих уравнений кривых 2ого порядка к каноническому виду:

Окружность: (x-α)^2 + (y-β)^2 =R^2

Эллипс: х^2 /a^2 + y^2/b^2 =1; e=c/a; c=√a^1 – b^2

Гипербола: х^2 /a^2 - y^2/b^2 =1; полуось а действительна.

х^2 /a^2 + y^2/b^2 = -1, полуось в действительна ; F1(0, -c) F2(0,c).

Парабола: а)у^2 = 2px; y=-p/2 ; в) x^2 = 2py; x=-p/2

12.Различные методы решения системы линейных уравнений: а)правило Крамера; в)с помощью обратной матрицы:

правило Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы.

Найдем определитель обычной матрицы,затем определитель дельта х получаемый из дельта путем замены первого столбца коэффициентов столбцом из свободных членов: х1=дельтах1/дельта.Аналогично с дельтау.

Обра́тная ма́трица — такая матрица A^−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E.

Выведем матричную формулу.Умножив обе части уравнения АХ=В слева на матрицу А^-1,получим А^-1 *АХ=А^-1 *В,поскольку А^-1 *А=Е и ЕХ=Х, то Х=А^-1 *В.

13.Функция.Предел функции и его свойства Сравнение функции.Бесконечно малые и большие величины.

функция-это зависимость, при которой каждому значению аргумента соответствует единственное значение функции.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции в точке:Число А назыв.пределом функции у=f(x) в точке а=х0 если любое Е>0,найдет такое δ=δ(Е)>0;любое х : х неравно а,удовлет.│х-а│<Е выполняется нед.│ f(x)-А│<Е →lim(х→а) f(x)=A

Свойства пределов функции:

1) Предел постоянной величины.Предел постоянной величины равен самой постоянной величине

2) Предел суммы.Предел суммы двух функций равен сумме пределов этих функций

3) Предел произведения функции на постоянную величину.Постоянный коэффициент можно выносить за знак предела

4) Предел произведения.Предел произведения двух функций равен произведению пределов этих функций

5) Предел частного.Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Свойства:1)алгебраическая сумма конечного числа бес.мал.есть величина бес.мал. 2)произведение беск.мал.на аграниченную функцию есть величина беск.мал. 3)частное от деления бес.мал.на функц.предел не равен 0 есть величина беск.мал. 4) если: предел хстремится к бесконечности бескон.мал(0)/ϕ(х) = 0;бесконечн. Если: предел хстремит.к бесконечн. Беск.мал.(х)/ϕ(х) =1,то беск.мал и ϕ эквивалентные

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Свойства:1)произвед.ББВ на функцию предел неравен 0,есть величина бескон.больш. 2)сумма ббв и ограниченной функции есть величина бескон.больш. 3)частное от деления ббв на функцию предел в точке 0 есть величина беск.больш.

14. замечательные пределы

Первый замечательный предел:

Второй замечательный предел:

15 Алгебраическое уравнение 2-го порядка с 3-мя аргументами:

Аx^2+Вy^2+Cz^2+2Dxy+2Fyz+2Mx+2Ny+2Pz+Q=0

В пространстве оно определяет поверхности 2-го порядка. Это уравнение может быть приведено к одному из следующих случаев.

Пусть функция у = f(x) определена в точке x_0 и в некоторой окрестности этой точки. Функция y = f(x) называется непрерывной в точке x_0, если существует предел функций в этой точке и он равен значению функции в этой точке, т.е.:

lim┬(x→x_0 )⁡〖f(x)=f(x_0 )〗

Функция y = f(x) называется непрерывной в точке x_0, если она определена в точке x_0 и ее окрестности и выполняется равенство lim┬(∆x→0)⁡〖∆y=0〗 т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

Свойства односторонних пределов:

1)Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределом вдоль фильтра.

2)Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.

Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.

Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Говорят, что функция f(x) имеет точку разрыва первого рода при x = a, если в этой точке:

1)Существует левосторонний предел lim┬(X→a-0)⁡〖f(x)〗 и правосторонний предел lim┬(X→a+0)⁡〖f(x)〗

2)Эти односторонние пределы конечны.

При этом возможно следующие два случая:

3)Левосторонний предел и правосторонний предел равны друг другу:

lim┬(х→a-0)⁡〖f(x)〗=lim┬(х→a+0)⁡〖f(x)〗

Такая точка называется точкой устранимого разрыва.

4)Левосторонний предел и правосторонний предел не равны друг другу:

lim┬(х→a-0)⁡〖f(x)〗≠lim┬(х→a+0)⁡〖f(x)〗

Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов |lim┬(х→a-0)⁡〖f(x)〗-lim┬(х→a+0)⁡〖f(x)〗 | называется скачком функции.

Функция f(x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

16. Пусть функция x = φ(t) имеет обратную функцию t = Ф(x). Если функции x=φ(t), y = ψ(t) дифференцируемы и φ'(t) ≠ 0, тогда

Производная сложной функции:

17. Дифференциал функции – это произведение производной и приращения аргумента

Теорема 1. Если функция дифференцируема в некоторой точке, то в этой точке она имеет дифференциал.

Теорема 2. Если функция имеет дифференциал в некоторой точке, то она имеет производную в этой точке.

18 Дифференциалы высших порядков.

Пусть в интервале (а, b) задана дважды дифференцируемая функция y = f(x), где x – независимая переменная.

Фиксируем приращение dx= ∆x независимой переменной x, т.е. будем считать первый дифференциал dy=f^' (x)dx функцией только переменной x.

19. 1. Область определения

2. Исследование функции на четность, нечетность и периодичность

Если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство , то – четная функция; если область определения функции симметрична относительно нуля и для любого x из области определения выполнено равенство , то – нечетная функция; в противном случае, – общего вида. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.

3. Нахождение точек пересечения графика функции с осями координат

4. Нахождение промежутков знакопостоянства функции.Промежутки знакопостоянства функции – промежутки из области определения функции, где функция принимает положительные или отрицательные значения

5. Нахождение производной функции, области определения производной, критических точек.Критические точки функции – внутренние точки области определения функции, в которых производная не существует или равна нулю.

6. Нахождение промежутков возрастания, убывания, точек экстремума и экстремумов.Критические точки функции разбивают область определения функции на промежутки. Для нахождения промежутков возрастания, убывания и точек экстремума нужно определить знак производной на каждом из полученных промежутков. Если производная функции положительна на некотором промежутке I, то функция возрастает на этом промежутке; если производная функции отрицательна на некотором промежутке I, то функция убывает на этом промежутке. Если при переходе через критическую точку производная меняет знак, то данная точка является точкой экстремума.

7. Нахождение промежутков выпуклости функции и точек перегиба.Для нахождения промежутков выпуклости используется вторая производная функции. Точки, в которых вторая производная равна нулю или не существует, разбивают область определения функции на промежутки.

8. Исследование поведения функции на бесконечности и в окрестности точек разрыва

Для исследования поведения функции в окрестности точки разрыва необходимо вычислить односторонние пределы: и . Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая – вертикальная асимптота.При исследовании поведения функции на бесконечности необходимо проверить, не имеет ли график функции наклонных асимптот при и . Для этого нужно вычислить следующие пределы: и . Если оба предела существуют, то – уравнение наклонной асимптоты при . Частный случай наклонной асимптоты при – горизонтальная асимптота. Аналогично ищется наклонная асимптота при .

9. Построение графика (при необходимости нужно найти значения функции в дополнительных точках)

20 Пусть a является некоторым конечным действительным числом или равно бесконечности.

Если и , то ;

Если и , то аналогично

Правило Лопиталя

Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть lim┬(x→a)⁡〖f(x)=lim┬(x→a)⁡〖g(x)= 0〗 〗 или lim┬(x→a)⁡〖f(x)=lim┬(x→a)⁡〖g(x)= ∞〗 〗. Тогда, если существует предел отношения производных этих функции lim┬(x→a)⁡〖(f'(x))/(g'(x))〗 , то существует и предел отношения самих функции (f(x))/(g(x)) при x→a, причем

lim┬(x→a)⁡〖f(x)/g(x) 〗= lim┬(x→a)⁡〖(f^' (x))/(g^' (x) )〗

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом:

предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

21 Определение первообразной и неопределенного интеграла

Функция F(x) называется первообразной функции f(x), если

Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как

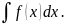
Таким образом, если F – некоторая частная первообразная, то справедливо выражение

Свойства неопределенного интеграла.

В приведенных ниже формулах f и g – функции переменной x, F – первообразная функции f, a, k, C – постоянные величины.

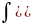
22. Методы интегрирования неопределенных интегралов.

Метод подстановки

Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной. Он основан на следующей теореме.

Метод интегрирования по частям

Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.

 Интегрирование дробно-рациональных функций

Пусть   и   некоторые полиномы степени m и n

Функция вида

называется дробно-рациональной функцией

рациональной дробью называется отношение 2ух многочленов.

23 Интегралы вида

находятся с помощью тригонометрических формул

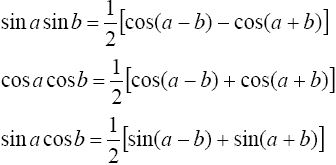
2°. Интегралы вида

где m и n - четные числа находятся с помощью формул понижения степени

Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

24. Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.

Если функция интегрируема на [a; b], то она интегрируема на любом отрезке

Для любых a, b и c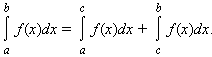

Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A

Если f (x) и g (x) интегрируемы на [a; b], то f (x) · g (x) также интегрируема на этом отрезке.

Если f (x) – периодическая функция с периодом T, то д

Формула Ньютона-Лейбница

Если непрерывна на отрезке и — ее любая первообразная на этом отрезке, то имеет место равенство

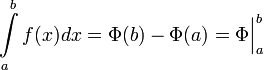
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:

Предел a или b (или оба предела) являются бесконечными;

Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].

25. . Операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев с помощью весьма простых средств решать сложные математические задачи.

ПРЕОБРАЗОВАНИЯ ЛАПЛАСА

Функцией-оригиналом называется комплекснозначная функция f (t) действительного аргумента t, удовлетворяющая условиям:

1. f (t) интегрируема на любом конечном интервале оси t;

2. f (t)=0 для всех отрицательных t;

3. f (t) возрастает не быстрее показательной функции, т. е. существуют такие постоянные М и s0, что |f(t)|<Mes0t для всех t.Изображением функции f (t) (по Лапласу) называется функция F(p) комплексного переменного p=s +it , определяемая равенством

Тот факт, что F(p) есть изображение f (t), будем символически записывать так:

Для любой функции-оригинала f (t) изображение определено в полуплоскости Rep>s0 и является в этой полуплоскости аналитической функцией.

Из определения изображения следуют его простейшие свойства:

1. Линейность. Для любых комплексных постоянных a и b

(здесь и далее считать f(t)=F(p), g(t)=G(p)).

2.Теорема подобия. Для любого постоянного a >0

.

3. Дифференцирование оригинала. Если функции f (t), fў (t) , fІ (t),…, f (n)(t) являются функциями-оригиналами и f(t)=F(p), то

,

, ,где под f (k)(0), (k= 1, 2,…, n-1) понимается .

4. Дифференцирование изображения. Дифференцирование изображения сводится к умножению на (-t) оригинала

или вообще

.

5. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р, т. е. если f(t)=F(p), то

6. Интегрирование изображения. Если интеграл сходится, то он служит изображением функции

7.Теорема смещения. Если f(t)=F(p), то для любого комплексного р0

8.Теорема запаздывания. Если f(t)=F(p), то для любого t >0

Важной для приложений является следующая:

Теорема единственности

Если две функции j(t) и j(t) имеют одно и то же L-изображение F(p), то эти функции тождественно равны.