13. Свойства непрерывных функций. Понятие равномерной непрерывности функции.

Основные свойства непрерывных функций

Теорема (об устойчивости знака непрерывной

функции)

Пусть функция f(x) непрерывна в точке х0 и

f(x0) ¹ 0. Тогда существует d > 0 такое, что для

всех хÎ(х0 – d, х0+d) функция f(x) имеет тот же

знак, что f(x0).

Доказательство: Пусть f(x0) > 0. Тогда в силу определения 2 непрерывности функции для "e>0 d$>0 такое, что неравенство |f(x) – f(x0)|<e выполняется для всех х, удовлетворяющих неравенству |x – x0| < d.

Или f(x0) – e < f(x) < f(x0) + e для всех хÎ(х0 – d, х0 + d). Возьмем e = f(x0). Тогда f(x) > 0 для всех х Î (х0 – d, х0 + d). Ч.т.д.

Теорема (1-ая теорема Больцано-Коши) Пусть функция f(x) непрерывна на отрезке [a,b] и на концах отрезка имеет значения разных знаков. Тогда существует точка с(a,b), в которой f(с) = 0.

Доказательство:

Пусть для определенности f(a)<0 и f(b)>0. Разделим [a,b] пополам. Если значение функции в середине [a,b] равно нулю, то теорема доказана. В противном случае выберем тот из двух полученных отрезков, на концах которого f(x) имеет значения разных знаков, обозначим его [a1,b1]. Разделим его пополам. Если значение функции в середине отрезка [a1, b1] равно нулю, то теорема доказана. В противном случае выберем тот из двух полученных отрезков, на концах которого f(x) имеет значения разных знаков. Обозначим его [a2, b2]. И т.д. Получим последовательность [a,b]É[a1, b1]É[a2, b2]É…É[an, bn]É… вложенных отрезков. По теореме о вложенных отрезках $с, принадлежащая всем отрезкам, причем f (с)=0. Ч.т.д. Теорема имеет простой геометрический .смысл.

Теорема (вторая теорема Больцано-Коши)

Пусть функция f(x) непрерывна на отрезке [a, b], причем f(a) = A, f(b) = B. Пусть С – любое число, заключенное между А и В.

Тогда на отрезке [a, b] найдется точка с такая, что f(с) = С.

Другими словами, непрерывная функция при переходе от одного значения к другому принимает и все промежуточные значения.

Теорема (первая теорема Вейерштрасса)

Если функция f(х) определена и непрерывна на отрезке

[a,b], то она ограничена на этом отрезке.

Замечание.

Теорема неверна, если отрезок [a, b] заменить интервалом

(а, b).

Теорема (вторая теорема Вейерштрасса)

Если функция f(x) непрерывна на отрезке [a, b], то она

имеет на этом отрезке наибольшее и наименьшее

значения.

Замечание

Разность между наибольшим и наименьшим значениями

непрерывной функции f(x) на отрезке [a, b] называется

колебанием непрерывной функции.

Понятие равномерной непрерывности функции

Определение. Функция f(х) называется равномерно-

непрерывной на промежутке Х, если для любого e > 0

существует d > 0 такое, что для любых двух точек х1, х2 ÎХ,

удовлетворяющих неравенству |x2 – x1| < d, выполняется

неравенство |f(х2) – f(x1)| < e.

С имволика:

Теорема Кантора (о равномерной непрерывности)

Если функция f(x) непрерывна на отрезке [a, b], то она и

равномерно непрерывна на нем.

14. производная функции, определение, геометрический смысл. Уравнения касательной и нормали. Правила вычисления производных. Логарифмическая производная. Таблица производных простейших элементарных функций.

Понятие производной

Определение. Производной функции y = f(x) в точке х0 называется предел при Dх ® 0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует).

Пример: Вычислить производную функции y = x2 в точке х = 5.

Е

или

сли для некоторого значения х0 выполняется условие то говорят, что в точке х функция имеет бесконечную производную знака «+» или знака «–». В отличие от бесконечной производной определенную выше производную функции иногда называют конечной производной.

Г еометрический смысл производной

Касательная к кривой – прямая, имеющая с кривой единственную общую точку.

Определение. Касательной к графику функции y = f(x) в точке М называется предельное положение секущей MN, когда точка N стремится к точке М по кривой f(x).

Уравнения касательной и нормали к кривой

Производная f’(x0) равна угловому коэффициенту (тангенсу угла наклона к положительному направлению оси Ох) касательной к графику функции y = f(x) в точке M(x0, f(x0)). При этом

Для касательной всегда выполнятся

Е сли взять

Уравнение касательной:

О пределение. Нормалью к кривой называется прямая, проходящая через точку касания перпендикулярно касательной.

Для перпендикулярных прямых

Уравнение нормали к кривой:

Физический смысл производной

Если функция s = f(t) описывает закон движения материальной точки по прямой как зависимость пути от времени, то

Путь, пройденный за интервал времени Dt.

С редняя скорость за время Dt

Мгновенная скорость точки

В определенном смысле производную функции y = f(x) можно также трактовать как скорость изменения функции: чем больше величина f’(x), тем больше угол наклона касательной к кривой, тем круче график f(x) и быстрее растет функция.

П равая и левая производные

Пример:

Рассмотрим точку x = 0

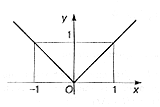
Операцию нахождения производной называют дифференцированием. Функция, имеющая производную в точке, называет дифференцируемой в этой точке.

Определение. Функция f(x) называется дифференцируемой в точке х0, если ее приращение в этой точке можно представить в виде Dy = A×Dx + a(Dx)D×x, где А – некоторое число, не зависящее от Dх, а a(Dх) – функция аргумента Dх, являющаяся бесконечно малой при Dх®0, т.е.

Теорема Если функция f(x) дифференцируема в данной точке х0, то она и непрерывна в этой точке.

Замечание. Обратное утверждение неверно. Например, функция f(x) = |x| непрерывна в точке х = 0, но не является дифференцируемой.

Таким образом, требование дифференцируемости является более сильным, чем требование непрерывности.

Правила дифференцирования суммы, разности, произведения и частного

Т еорема. Если функции u = u(x) и v = v(x) дифференцируемы в точке х, то сумма, разность, произведение и частное этих функций (частное при условии v(x) ¹ 0) также дифференцируемы в этой точке и имеют место следующие формулы

Т еорема о производной обратной функции Пусть функция х = j(у) является обратной для функции y = f(x). Теорема. Если функция y = f(x) имеет в точке х0 производную f(x) ¹ 0, то обратная функция х = j(у) также имеет в соответствующей точке у0 = f(x0) производную, причем

Д оказательство. Учтем, что Перейдем к пределу при Dу ® 0. Обратная функция х = j(у) непрерывна в точке у0, то Dх ® 0 при Dу ® 0. Получим

Т еорема имеет простой геометрический смысл и отражает очевидный факт:

Правило дифференцирования сложной функции

Т еорема. Если функция u = j(x) имеет производную в точке x0, а функция y = f(u) имеет производную в соответствующей точке u0 = j(x0), то сложная функция f [j(x)] имеет производную в точке x0 и справедлива следующая формула

Доказательство: т.к. функция y = f(x) дифференцируема в точке х0, то

Т ак как по условию u = j(x) дифференцируема, то она и непрерывна в точке x0, следовательно

При и

Переходя к пределу в предыдущем равенстве получим

Замечание. Правило дифференцирования остается тем же, если зависимость более сложная – с двумя, тремя и большим числом промежуточных переменных.

Производные простейших элементарных функций

На основе правил и формул дифференцирования можно сделать вывод: операция дифференцирования не выводит из класса элементарных функций.

Логарифмическая производная

Вычислим производную сложной функции

которая называется логарифмической производной (знак модуля обычно не записывается).

Л огарифмическую производную удобно использовать при нахождении производных функций, выражения которых значительно упрощаются при логарифмировании.

Пример. Степенно-показательная функция

Техника нахождения производных

Основные правила:

• Ввести функцию u(x), так чтобы y = f(u) содержалось в таблице производных

• Использовать правила дифференцирования

П римеры: