- •1. Множества и действия с ними. Понятие множества и его элемента. Числовые множества. Задание множества. Операции над множествами и их свойства. Диаграммы Эйлера-Венна.
- •2. Действительные числа. Определение действительного числа, отношение порядка на множестве действительных чисел и его свойства, точная верхняя (нижняя) грани.
- •3.Комплексные числа. Определение комплексного числа, действия с комплексными числами. Тригонометрическая форма комплексного числа. Формула Муавра. Корень n-ой степени. Решение квадратного уравнения.
- •4. Понятие числовой функции: определение, способы задания, свойства, элементарные функции.
- •5. Числовые последовательности: определение, способы задания, арифметические действия над последовательностями.
- •6. Предел числовой последовательности: определение, свойства сходящихся последовательностей.
- •7. Бесконечно малые и бесконечно большие числовые последовательности. Основные свойства бесконечно малых последовательностей.
- •8. Теоремы о пределе суммы, разности, произведения и частного двух последовательностей. Основные теоремы о пределах числовых последовательностей.
- •9. Числовые ряды. Сумма числового ряда. Сходящиеся числовые ряды. Необходимый признак сходимости, абсолютно сход. Достаточные признаки сходимости.
- •10. Предел функции в точке. Односторонние пределы. Предел на бесконечности. Бесконечно малые и большие функции в точке, их свойства.
- •11. Основные теоремы о пределе функции в точке. Первый и второй замечательный пределы.
- •12. Непрерывные функции. Определение, теорема о непрерывности суммы, разности, пр-ия и частного двух функций. Характеристика точек разрыва функции.
- •1 .1. Через односторонние пределы:
- •13. Свойства непрерывных функций. Понятие равномерной непрерывности функции.
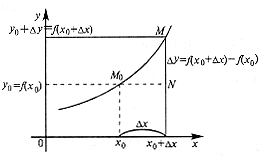
- •15. Дифференциал функции, определение, геометрический смысл. Производные высших порядков. Производные функций, заданных параметрически и неявно.
- •16. Теоремы о дифференцируемых функциях. Теоремы Ферма, Ролля, Лагранжа. Правило Лопиталя.
- •17. Локальные минимумы и максимумы. Необходимые и достаточные условия. Исследование функции на экстремумы.
- •18. Приложения производной в экономической теории.
11. Основные теоремы о пределе функции в точке. Первый и второй замечательный пределы.
Основные теоремы о пределах
Т1. (О единственности предела)
Если функция f(x) имеет предел в точке а, то этот предел единственный.
Т2. (О предельном переходе в неравенстве )
Пусть функции f(x) и g(x) определены на одном и том же промежутке Х и существуют пределы этих функций в т. а
![]()
Кроме того, существует такое число d > 0, что для всех х из d-окрестности числа а f(x) ³ g(x). Тогда A ³ B.
Т3. (Об ограниченности функции имеющей предел)
Е![]() сли
функция f(x)
имеет конечный предел в точке а,
то существуют числа М
> 0
и d
> 0 такие, что для
всех х
из d-окрестности
точки а
сли
функция f(x)
имеет конечный предел в точке а,
то существуют числа М
> 0
и d
> 0 такие, что для
всех х
из d-окрестности
точки а
Т![]() 4.
Пусть функции f(x),
g(x)
и h(x)
определены в некоторой окрестности
точки а,
за исключением, быть может, самой точки
а,
функции f(x)
и h(x)
имеют в точке а
предел, равный А,
т.е.
4.
Пусть функции f(x),
g(x)
и h(x)
определены в некоторой окрестности
точки а,
за исключением, быть может, самой точки
а,
функции f(x)
и h(x)
имеют в точке а
предел, равный А,
т.е.
![]()
Тогда если f(x) £ g(x) £ h(x), то
Т5. (Связь предела с алгебраическими операциями)
Пусть функции f(x) и g(x) имеют в точке а пределы В и С. Тогда функции f(x) ± g(x), f(x) × g(x) и f(x)/g(x) (при С ¹ 0) имеют в точке а пределы, равные В ± С, В × С и B/C соответственно.
Н![]() екоторые
важные пределы
екоторые
важные пределы
1.
![]()
2 .
Первый замечательный
предел:
.
Первый замечательный
предел:
![]()
![]()
![]()
![]()
3![]()
![]() .
Второй замечательный предел
.
Второй замечательный предел
Или
![]()
Делая замену переменной, имеем
![]()

4.
12. Непрерывные функции. Определение, теорема о непрерывности суммы, разности, пр-ия и частного двух функций. Характеристика точек разрыва функции.
Непрерывность функции
О![]() пределение
1. Функция f(x)
называется непрерывной
в точке x0,
если предел этой функции и ее значение
в этой точке равны, т.е.
пределение
1. Функция f(x)
называется непрерывной
в точке x0,
если предел этой функции и ее значение
в этой точке равны, т.е.
1 .1. Через односторонние пределы:
1![]() .2.
На языке e
– d
.2.
На языке e
– d
Определение 2 (на языке последовательностей). Функция f(x) называется непрерывной в точке х0, если для любой последовательности значений аргумента {xn}, сходящейся к х0, последовательность соответствующих значений функций {f(xn)} сходится к f(x0).
Е![]()
![]() сли
то
функцию f(x)
называют непрерывной в точке х0
справа (слева). Если функция f(x)
непрерывна в точке х0
и справа и слева, то она непрерывна в
этой точке.
сли
то
функцию f(x)
называют непрерывной в точке х0
справа (слева). Если функция f(x)
непрерывна в точке х0
и справа и слева, то она непрерывна в
этой точке.
Определение 3. Функция f(x) непрерывна в точке х0, если
![]()
Арифметические действия над непрерывными функциями
Теорема. Пусть функции f(x) и g(x) непрерывны в точке х0.
Тогда функции f(x) ± g(x), f(x)×g(x) и f(x)/g(x) также
непрерывны в этой точке (последняя при g(x)¹0).
Доказательство. Теорема следует из определения
непрерывности функций.
К![]() лассификация
точек разрыва функций
лассификация
точек разрыва функций
Е![]() сли
существует , но функция
в точке x0
не определена, то разрыв функции в точке
называется устранимым.
сли
существует , но функция
в точке x0
не определена, то разрыв функции в точке
называется устранимым.
Пример.
Определение. Точка х0 называется точкой разрыва
функции f(x), если f(x) в точке х0 не является непрерывной.
Точка х0 называется точкой разрыва 1-го рода функции
f(x), если в этой точке функция имеет конечные, но не
равные друг к другу правый и левый пределы:
![]()
Определение. Точка х0 называется точкой разрыва 2-го рода функции f(x), если в этой точке функция не имеет по крайней мере одного из односторонних пределов или хотя бы один из них из односторонних пределов бесконечен. Определение. Функция называется кусочно-непрерывной на отрезке [a,b], если она непрерывна во всех внутренних точках [a,b], за исключением, быть может, конечного числа точек, в которых имеет разрыв 1-го рода и, кроме того, имеет односторонние пределы в точках а и b. Определение. Функция называется кусочно-непрерывной на числовой прямой, если она кусочно-непрерывна на любом отрезке.