10. Предел функции в точке. Односторонние пределы. Предел на бесконечности. Бесконечно малые и большие функции в точке, их свойства.

Предел функции

Предел по Гейне:

Число А называется пределом функции f(x) в точке а, если для любой, сходящейся к точке а последовательности значений аргумента х (отличных от а), соответствующая последовательность значений функции сходится к числу А.

Предел по Коши:

Число А называется пределом функции f(x) в точке а, если для любого e-окрестности точки А, можно найти проколотую d-окрестность точки а, такую, что для всех х из этой окрестности соответствующие значения функции принадлежат e-окрестности точки А.

О пределение без использования окрестностей (на языке e - d ):

Замечания:

1. Использование в определении предела проколотой окрестности является существенным, т.к. сама функция может и не существовать в точке а.

2 . Можно обобщить понятие предела, если под а и А понимать не только числа, но и и использовать соответствующие окрестности.

3. В отличие от последовательностей говорить о пределе функции без указания точки, в которой вычисляется предел бессмысленно! Функции имеют в разных точках различные пределы!

Геометрическая иллюстрация:

Примеры:

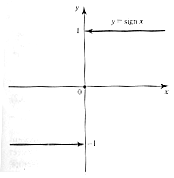
Данная функция не имеет

предела в точке а = 0

Это означает, что не

существует e такое, что

для любого числа А не

существует нужного нам

числа d

Односторонние пределы

Определение 1. Число А называется правым (левым) пределом функции f(x) в точке а, если для любой сходящейся к а последовательности x1, x2, …, xn, … такой, что xn > a (xn < a), соответствующая последовательность f(x1), f(x2), …, f(xn), … сходится к А.

Определение 2. ( на языке e-d ) Число А называется правым (левым) пределом функции в точке а, если для любого e>0 существует такое d>0, что для всех х из правой (левой) d-окрестности точки а, т.е. a<x<a+d ( a-d <x<a), выполняется неравенство |f(x) – A|< e. Теорема. Функция f(x) имеет в точке а предел тогда и только тогда, если в этой точке существуют правый и левый пределы, причем они равны. В этом случае предел функции равен односторонним пределам.

Пример:

Различные виды пределов

Пределы на бесконечности:

Определение 1. Число А называется пределом функции f(x) при х®+¥ , если для любой бесконечно большой последовательности значений аргумента x1, x2, …, xn, … ( xn >0 ) соответствующая последовательность значений функции f(x1), f(x2), …, f(xn), … сходится к А.

Число А называется пределом функции f(x) в + бесконечности, если для любой e-окрестности точки А, можно найти N-окрестность + бесконечности, такую, что для всех х из этой окрестности соответствующие значения функции принадлежат e-окрестности точки А.

Бесконечные пределы: (бесконечно большие функции)

Функция f(x) имеет в точке а предел равный плюс бесконечности (является положительной бесконечно большой в окрестности точки а ), если для любой N-ок-рестности плюс бесконечности, можно найти проколотую d-окрестность точки а, такую, что для всех х из этой окрестности соответствующие значения функции принадлежат N-окрестности плюс бесконечности.

Функция f(x) называется бесконечно малой в окрестности точки а (в точке а), если ее предел в этой точке равен 0.

Теорема. Для того, чтобы функция f(x) имела конечный предел в точке а необходимо и достаточно, чтобы функция a(х) = f(x) – A была бесконечно малой при х ® а.

Свойства бесконечно малых:

• Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

• Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая

• Величина обратная бесконечно малой есть величина бесконечно большая

• Величина обратная бесконечно большой есть величина бесконечно малая

Сравнение бесконечно малых и бесконечно больших функций

П усть при х ® а функции a(х) и b(х) являются бесконечно малыми. Тогда: 1) если , то a(х) – бесконечно малая более высокого порядка, чем b(х). 2) если (А – число), то a(х) и b(х) – бесконечно малые одного порядка.

3 ) если , то a(х) и b(х) – эквивалентные бесконечно

м алые. Обозначается: a(х) ~ b(х)

4) если , то a(х) – бесконечно малая n-го

порядка относительно b(х).

Т еорема. Если a(х) ~ a1(х) и b(х) ~ b1(х) при х ® а и существует , то существует причем

Примеры эквивалентных бесконечно малых (при x ® 0):

Сравнение бесконечно больших функций:

Для бесконечно больших функций также имеют место аналогичные правила, учитывая, что вместо термина “порядок малости” употребляется термин “порядок роста”.