8. Теоремы о пределе суммы, разности, произведения и частного двух последовательностей. Основные теоремы о пределах числовых последовательностей.

Теоремы о пределах суммы, разности, произведения и частного последовательностей:

• Сумма(разность) сходящихся последовательностей есть сходящаяся последовательность, предел которой равен сумме(разности) пределов исходных последовательностей.

• Произведение сходящихся последовательностей есть сходящаяся последовательность, предел которой равен произведению пределов исходных последовательностей.

• Частное двух сходящихся последовательностей при условии отличия знаменателя от нуля есть сходящаяся последовательность, предел которой равен частному пределов исходных последовательностей.

Примеры:

1.

2.

3.

Основные теоремы о пределах

Т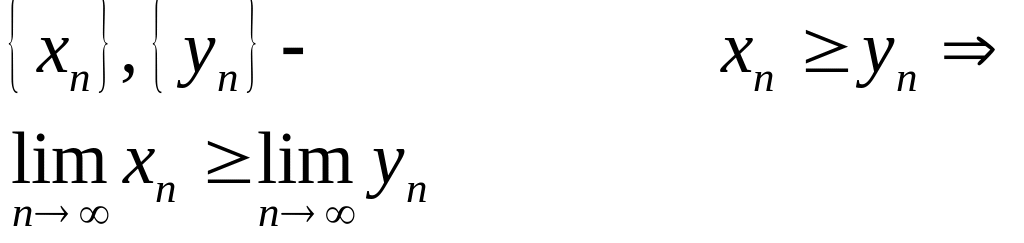 .1. (О предельном переходе в неравенстве )

Сходятся, причем

Замечание: Если вместо нестрогого неравенства выполнятся строгое, то гарантировать выполнение строгого неравенства для пределов нельзя! (они могут быть и равны)

Т.2. Сравнительный признак сходимости («о двух милиционерах»)

Е сли сходящиеся последовательности xn, yn, zn таковы, что

П ример:

Н екоторые важные пределы

1. 2.

.

3. число е:

Основные виды неопределенностей

Тождественные преобразования при вычислении пределов

9. Числовые ряды. Сумма числового ряда. Сходящиеся числовые ряды. Необходимый признак сходимости, абсолютно сход. Достаточные признаки сходимости.

Сходимость и сумма числового ряда

Определение. Числовой ряд – сумма элементов бесконечной числовой последовательности:

un – общий или n-й член ряда

n-я частичная сумма ряда -

Сходящийся ряд: (S – сумма ряда)

Р асходящийся ряд: или не $

Примеры числовых рядов

Свойства сходящихся рядов

1. Отбрасывание конечного числа членов не влияет

на сходимость.

2. Если ряд сходится и имеет сумму S, то сходится

т акже и ряд (a ¹ 0 – число)

причем сумма этого ряда равна aS.

3. (Необходимое условие сходимости ряда)

Если ряд сходится, то

4 . Если два ряда сходятся

то сходится и ряд

Замечание

3-е свойство является необходимым, но не достаточным

Достаточные признаки сходимости

Ряды с неотрицательными членами

Основное свойство: последовательность частичных сумм ряда является неубывающей

Необходимое и достаточное условие сходимости: Для того, чтобы ряд сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

П ризнаки сравнения

Теорема. Пусть для двух рядов с неотрицательными членами

Т огда из сходимости ряда bn следует сходимость ряда an. А расходимость ряда an влечет за собой расходимость bn.

Док-во: Рассмотрим частичные суммы рядов

Пример 1: пример 2

Пример 3 (ряд Дирихле)

При a = 1 ряд называется гармоническим. Ряд Дирихле сходится при a > 1 и расходится a £ 1.

Предельный признак сравнения

Теорема. Если для двух рядов с положительными членами

То оба ряда сходятся и расходятся одновременно.

П ризнак Даламбера

Теорема. Пусть для ряда с положительными членами существует

Тогда этот ряд сходится при r < 1 и расходится при r > 1.

Примеры применения признака Даламбера

r = a

r = e > 1 Þ ряд расходится

П ризнак Коши

Теорема. Если существует предел То ряд сходится при L < 1 и расходится при L > 1.

П ример 1:

Пример 2:

Знакопеременные ряды

знакочередующийся ряд -

Признак Лейбница: Если последовательность абсолютных величин членов знакопеременного ряда является невозрастающей и общий член ряда стремится к нулю, то ряд сходится.

Д оказательство:

последовательность монотонно возрастающая :

последовательность ограничена :

Замечание. В признаке Лейбница существенны оба условия!!

С ложим каждые два члена и получим расходящийся ряд:

Следствие:

Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, по абсолютной величине не превышает абсолютной величины первого отброшенного члена

П ример: Какое число членов ряда необходимо взять, чтобы вычислить его сумму с точностью до 0,001?

Абсолютная и условная сходимость

(1) -Абсолютно сходящийся ряд, если сходится (2)

(1) – условно сходящийся ряд, если ряд (2) расходится

Примеры:

Различие свойств абсолютно и условно сходящихся рядов

Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.

Условно сходящиеся ряды такими свойствами не обладают.

П ример.