5. Числовые последовательности: определение, способы задания, арифметические действия над последовательностями.
Бесконечной числовой последовательностью называют функцию, заданную на множестве натуральных чисел N, с областью значений R.
О
бычно
используют обозначения
С
пособы
задания последовательностей:
Формула общего члена
Несколько
членов последовательностиРекуррентная формула:
- Арифметическая прогрессия
- Геометрическая прогрессия
Словесный
Виды последовательностей:
Монотонные последовательности (строго монотонные)
Ограниченные последовательности (сверху, снизу )
Арифметические операции над последовательностями:
Сумма/разность последовательностей
Произведение последовательностей
Умножение на число
Частное последовательностей
6. Предел числовой последовательности: определение, свойства сходящихся последовательностей.
Предел числовой последовательности
Число А называется пределом числовой последовательности {xn}, если для любого положительного числа e существует такой номер N = N(e) (возможно зависящий от e), что все члены последовательности с номерами, принадлежащими N-окрестности +¥, принадлежат e окрестности точки А.
Другой вид
Число А называется пределом последовательности {xn}, если в любой его e-окрестности находятся все элементы этой последовательности, начиная с некоторого номера N, зависящего от e.
П
оследовательности,
имеющие предел, называются сходящимися,
в противном случае – расходящимися.
П
ример
1 расходящейся
последовательности:
П
ример
2. Рассмотрим
последовательность
Д
окажем,
что предел этой последовательности А
= 2
П
ример
3. Рассмотрим
последовательность
Доказать, что предел этой последовательности существует и равен 1.
Доказать, что предел последовательности равен 1/2.
Основные свойства сходящихся последовательностей
Сходящаяся последовательность имеет только один предел
Доказательство (от противного):
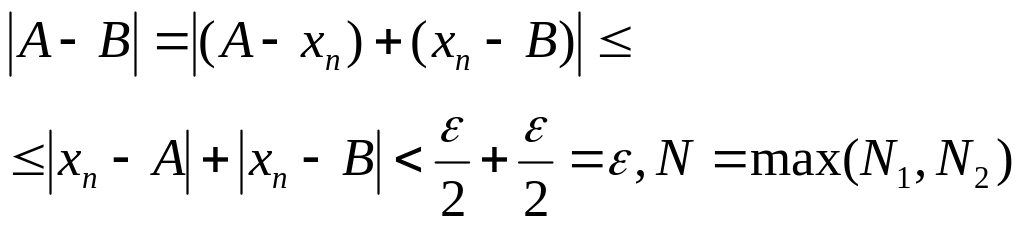
Любая сходящаяся последовательность является ограниченной.
Доказательство:
Если последовательность сходится, то сходится и любая ее подпоследовательность, и притом к тому же пределу.
Всякая монотонная ограниченная последовательность имеет предел.
Критерий Коши. Для того, чтобы последовательность имела предел необходимо и достаточно, чтобы в любой e окрестности нуля находилась разность между двумя произвольными членами этой последовательности, начиная с некоторых номеров, зависящих от e.
7. Бесконечно малые и бесконечно большие числовые последовательности. Основные свойства бесконечно малых последовательностей.
Бесконечно большие и бесконечно малые последовательности
Опр.: Последовательность {an}, имеющая предел равный нулю, называется бесконечно малой.
Опр.: Последовательность {xn} называется бесконечно большой, если для любого положительного числа А в A-окрестности бесконечности находятся все элементы этой последовательности, начиная с некоторого номера N, зависящего от А.
Теорема. Связь между бесконечно большими и бесконечно малыми.
Е
сли
{xn}
– бесконечно большая последовательность
и все
ее члены отличны от нуля, то последовательность бесконечно малая.
Е
сли
все элементы бесконечно малой
последовательности
{an } отличны от нуля, то последовательность
бесконечно большая.
З
амечание
о бесконечно большой величине:
Основные свойства бесконечно малых
Т1. Последовательность (переменную величину), имеющую предел можно представить в виде суммы своего предела и некоторой бесконечно малой величины.
Т2. Если переменную величину xn можно представить в виде суммы двух слагаемых: постоянного числа А и бесконечно малой величины, то числа А есть предел переменной величины xn.
Т3. Сумма и разность двух бесконечно малых являются бесконечно малыми.
Т4. Произведение двух бесконечно малых – бесконечно малая.
Т5. Произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью.
Доказательство:
Т
1.
Т3
Т
4
Т5