4. Понятие числовой функции: определение, способы задания, свойства, элементарные функции.

Понятие функции

П усть имеются два множества X и Y. Пусть далее указано правило, по которому каждому элементу сопоставляется некоторый (единственный) элемент

Т огда говорят, что задано отображение или, по-другому, функция из Х в Y.

f – есть отображение множества X в множество Y.

Д ля соответствующих элементов x и y используют запись:

x – независимая переменная (аргумент)

y – зависимая переменная

X – область определения (существования) функции

Y – область значений (изменения) функции

Если X и Y – числовые множества, то функция называется числовой

Ч исловая функция

График числовой функции:

Замечание: Каждая прямая x = const либо пересекает график в единственной точке, либо не пересекает его вовсе.

Способы задания функций

• Аналитический способ:

• Табличный

Графический

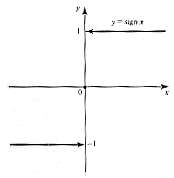
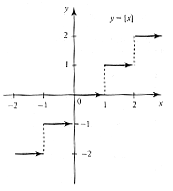
• Описательный (словесный)

Ц елая часть числа (ближайшее целое число, не превосходящее значение аргумента )

Основные свойства функций

• Ч етность и нечетность:

ч етная –

нечетная -

• Монотонность:

  • возрастающая (строго возрастающая)

• Убывающая (строго убывающая)

• О граниченность:

• П 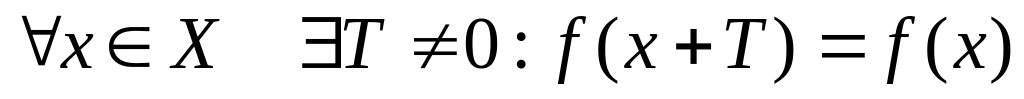ериодичность:

• Сложная функция (композиция функций) :

• Обратная функция:

Можно определить обратное отображение:

Элементарные функции

О сновные элементарные функции:

• С тепенные функции:

• Показательные функции:

• Л огарифмические функции:

• Т ригонометрические функции:

• Обратные тригонометрические функции

Действия над функциями

Допустимые действия над функциями:

• Все арифметические действия:

• Построение сложной функции

Элементарными функциями называются функции, полученные основных элементарных с помощью допустимых действий

Классификация элементарных функций

• Целые рациональные функции (алгебраический многочлен)

• Дробно-рациональные функции:

• Иррациональные функции:

Не рациональная функция, получаемая путем допустимых операций над степенными функциями с целыми и дробными показателями

• Трансцендентные функции:

В сякая функция не являющаяся рациональной или иррациональной

К ривые спроса и предложения

c, d – экзогенные величины

М – точка равновесия, Р0 – равновесная цена

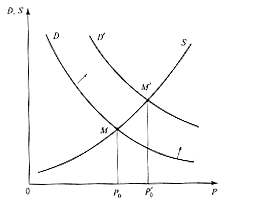
Увеличение благосостояния населения – рост величины с!

П ромежутки

• О трезок

• И нтервал

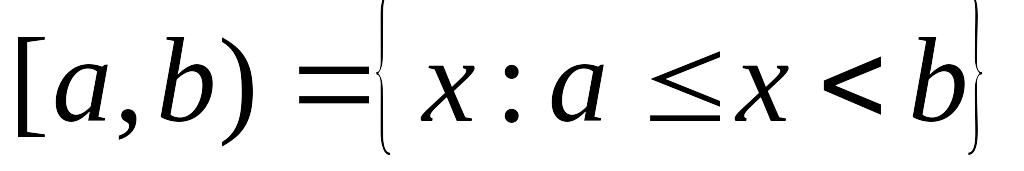• П олуоткрытый интервал

• П олубесконечный отрезок

Окрестности точки

d -окрестность точки a

Проколотая d-окрестность точки a

Л евая d-окрестность точки a

П равая d-окрестность точки a

N -окрестность

N -окрестность

N-окрестность