17. Локальные минимумы и максимумы. Необходимые и достаточные условия. Исследование функции на экстремумы.

Исследование поведения функции и построение графиков

Теорема (признак монотонности функции). Если функция f(x) дифференцируема на интервале (a, b) и f '(x) ³ 0 (f '(x) £ 0) на (a, b), то функция f(x) не убывает (не возрастает) на (a, b). Доказательство. Пусть х1 и х2 – произвольные точки из (a,b) и х1 < х2. Тогда имеем: f(x2) – f(x1) = f '(с) (x2 – x1), сÎ(a, b).

По условию f '(с)³0, х2 – х1> 0 Þ f(x2) – f(x1) ³0 Þ f(x2) ³ f(x1), т.е. функция f(x) не убывает на (a, b). Доказательство для случая f '(x) £0 аналогично.

Замечание. Точно также можно доказать, что если f '( x)>0 (<0) на (a, b), то f(x) возрастает (убывает) на (a, b). Это условие называется достаточным условием возрастания (убывания) функции f(x) на промежутке (a, b).

Отыскание точек локального экстремума функции

Определение. Точка х0 называется точкой строгого локального максимума (минимума) функции f(x), если для всех х из некоторой d-окрестности точки х0 выполняется неравенство f(x) < f(x0) (f(x) > f(x0)) при х ¹ х0. Локальный максимум (max) и локальный минимум (min) объединяются общим названием локальный экстремум.

Необходимое условие локального экстремума

Теорема. Если функция f(x) имеет в точке х0 локальный экстремум и дифференцируема в этой точке, то f '(x0) = 0. Доказательство: Т.к. в точке х0 функция f(x) имеет локальный экстремум, то существует такой интервал (x0 – d, x0 + d), в котором значение f(x0) является наибольшим или наименьшим среди всех других значений этой функции. Тогда по теореме Ферма f '(x0) = 0.

Замечание. Понятие экстремума носит локальный характер в том смысле, что неравенство f(x) < f(x0) (f(x) > f(x0)) может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки х0. Функция может иметь несколько локальных максимумов и локальных минимумов, причем может так случиться, что иной локальный максимум окажется меньше какого-то локального минимума.

Первое достаточное условие локального экстремума

Теорема. Пусть функция f(x) дифференцируема в некоторой окрестности точки х0. Если при переходе через эту точку слева направо производная f '(x) меняет знак с “+” на “-” ( c “-” на “+”), то в точке х0 функция f(x) имеет локальный максимум (минимум). Если же f '(x) не меняет знак в d-окрестности точки х0, то данная функция не имеет локального экстремума в точке х0.

Доказательство.

Пусть при переходе через точку х0 производная меняет знак с “+” на “-” в интервале (х0 - d, х0 + d). Возьмем произвольную точку х Î(х0 - d, х0), х ¹ х0; на отрезке [x, x0] выполняются условия: f(x0) - f(x) = f '(с)(х0 - х), сÎ(х, х0). Т.к. f '(x)>0 при хÎ(х0 - d, х0) и х0 >х, получим f(x) < f(x0). Возьмем точку хÎ(х0, х0 + d), х ¹ х0; на отрезке [x0, x] выполняются условия: f(x) - f(x0) = f '(с)(х - х0), сÎ(х0, х). Т.к. f '(х) < 0 при хÎ(х0, х0 + d) и х0 < x, получим f(x0) > f(x). Þ в d-окрестности точки х0 выполняется условие локального максимума.

Случай локального минимума доказывается аналогично.

Если же f '(x) не меняет знака при переходе через точку х0, то она является монотонной на интервале (х0 - d, х0 + d) Þ не имеет локального экстремума в точке х0.

Замечание. Теорема остается справедливой, если функция f(x) в самой точке х0 не дифференцируема, а только непрерывна. Например, функция f(x) = |x| в точке х = 0 непрерывна, но не дифференцируема.

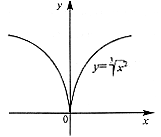
Необходимое условие экстремума: Для того, чтобы функция y = f(x) имела экстремум в точке х0, необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала. Такие точки называют критическими (или стационарными).

З амечание. Критическая точка вовсе не обязательно является точкой экстремума

Второе достаточное условие экстремума

Теорема. Если первая производная f '(x) дважды дифференцируемой функции равна нулю в некоторой точке x0, а f''(x0) в этой точке > 0, то точка x0 есть точка минимума функции f(x); если f ''(x0) < 0, то x0 – точка максимума.

Доказательство. Пусть f '(x0) = 0, а f'' (x0) > 0. Это означает, что f ''(x) = (f '(x))' > 0 также и в некоторой окрестности точки х0, т.е. f '(x) возрастает на на некотором интервале (a, b), содержащим точку х0. Но f '(x0) = 0, следовательно, на интервале (а, х0) f '(x0) < 0, а на интервале (х0, b) f '(x0) > 0. т.е. f '(x) при переходе через точку х0 меняет знак с минуса на плюс, т.е. х0 – точка минимума.

Схема исследования функции y = f(x) на экстремум:

1. Найти производную f '(x).

2. Найти критические точки функции, в которых

производная f '(x) = 0 или не существует.

3. Исследовать знак производной справа и слева от каждой

критической точки и сделать вывод о наличии экстремумов.

( 3a. Найти вторую производную f ''(x) и определить ее знак

в каждой критической точке. Сделать вывод о наличие

экстремумов в критических точках.)

4. Найти экстремумы функции.

Схема для отыскания наибольшего и наименьшего значений на отрезке [a, b]:

1. Найти производную f '(x). 2. Найти критические точки функции, в которых f '(x) = 0 или не существует. 3. Найти значения функции в точках экстремума и на концах отрезка [a, b] и выбрать из них наибольшее и наименьшее.

Общая схема исследования функций и построения их графиков

1. Найти область определения функции. 2. Исследовать функцию на четность-нечетность. 3. Найти вертикальные асимптоты. 4. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты. 5. Найти экстремумы и интервалы выпуклости функции и точки перегиба. 6. Найти точки пересечения с осями координат и некоторые дополнительные точки, уточняющие график.