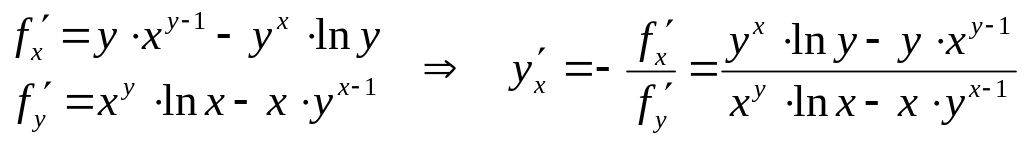15. Дифференциал функции, определение, геометрический смысл. Производные высших порядков. Производные функций, заданных параметрически и неявно.

Понятие дифференциала функции

П усть функция f(x) дифференцируема в точке х0, тогда её приращение в этой точке можно записать в виде суммы: Dy =A× Dx + a(Dx)D×x,

где

Слагаемое a(Dх)D×х при Dх ® 0 – бесконечно малая более высокого порядка, чем Dх.

О пределение. Дифференциалом функции y= f(x) в точке х0 называется главная, линейная относительно Dх, часть приращения функции в этой точке: dy = AD×x

Учитывая, что А=f '(x0), формулу можно записать в виде dy = f '(x0)×Dx. Дифференциалом независимой переменной х назовем приращение этой переменной dx = Dx. Соотношение принимает теперь вид: dy = f '(x0)dx

Геометрический смысл дифференциала

y

y

dy

M



y = f(x)

x



x

0

₀ x₀+x x

Производные высших порядков

Производная f '(x) функции y = f(x) сама является некоторой функцией аргумента х. Назовём f '(x) производной первого порядка функции f(x).

Производная от производной некоторой функции называется производной 2-го порядка (или второй производной) этой функции.

Производная от второй производной называется производной 3-го порядка (или третьей производной) и т.д.

П роизводные, начиная со второй, называются производными высших порядков и обозначаются у'', у''', у(4), …, у(n), … или f ''(x), f '''(x), f (4)(x), …,

f (n)(x), …

Производная n-го порядка является производной от производной (n-1)-го порядка:

y(n) = (y(n-1) )'.

Если функция y = f(x) описывает закон движения материальной точки по прямой линии, то 1-ая производная

f '(x) есть мгновенная скорость точки в момент времени х, а 2-ая производная равна ускорению точки в момент х

Производные, начиная со второй, называются производными высших порядков и обозначаются у'', у''', у(4), …, у(n), … или f ''(x), f '''(x), f (4)(x), …,

f (n)(x), …

Производная n-го порядка является производной от производной (n-1)-го порядка:

y(n) = (y(n-1) )'.

Параметрическое задание функции и ее дифференцирование

Пусть заданы две функции x = j(t), y = y(t) (1)

одной независимой переменной t, определенные и непрерывные в одном и том же промежутке.

Если x = j(t) строго монотонна, то обратная функция t = F(x) однозначна, также непрерывна и строго монотонна. Поэтому у можно рассматривать как функцию, зависящую от переменной х посредством переменной t, называемый параметром: y = y[F(x)].

В этом случае говорят, что функция у от х задана параметрически с помощью уравнений (1). Предположим, что функции (1) имеют производные, причем j'(t) ¹ 0 на некотором промежутке. По теореме о производной обратной функции функция F(x) имеет производную:

а по теореме о производной сложной функции функция y = y[F(x)] имеет производную:

y '(x) = y'[F(x)] × F '(x) Þ

Найдем вторую производную:

y''(x) = (y'(x))'x

Производная неявной функции

Функция задана неявно, если она имеет вид f(x, y) = C.

Для нахождения производной y'x заданной неявно функции нужно продифференцировать обе части уравнения, считая y = y(x), а затем из полученного уравнения найти производную y'x.

М ожно также воспользоваться свойством дифференциала функции двух переменных:

Производная неявной функции. Примеры