1. Множества и действия с ними. Понятие множества и его элемента. Числовые множества. Задание множества. Операции над множествами и их свойства. Диаграммы Эйлера-Венна.

Множество относится к первоначальным понятиям науки, не определяемым через другие, более простые термины.

Множество представляет собой определенную совокупность объектов, объединенных в единое целое в соответствии с некоторыми признаками и правилами. Множества обозначаются: A, B, C, X, Y, Z.

Примеры множеств: множество сотрудников фирмы;

множество всех атомов на Марсе; множество всех

натуральных чисел N; множество точек окружности.

Предметы, составляющие множество, называют его элементами. Элементы множеств обозначаются: a, b, c, x, y, z. Элементы множества и само множество связаны между собой отношением «принадлежность»: x Î A – элемент x принадлежит множеству A, x Ï A – элемент x не принадлежит множеству A.

Опр.1. Множество называется конечным, если оно

состоит из конечного числа элементов, и бесконечным – в

противном случае.

Опр.2. Если каждый элемент множества А является вместе с тем и элементом множества В, то А называется подмножеством множества В: А Í В - А содержится в В (или А включено в В) А подмножество В.Если А Í В и А ¹ В, то А называется собственным подмножеством множества В (обозначается А Ì В).

Опр.3. Множества А и В называются равными, если каждый элемент множества А является вместе с тем и элементом множества В, и каждый элемент В является элементом А: А = В А Í В и В Í А.Опр.4. Множество Æ, не содержащее ни одного элемента, называют пустым множеством. Очевидно, что " А Æ Í А.

Пример 1. Множество решений уравнения x2 + 1 = 0 во множестве действительных чисел – пустое множество Æ.

Опр.5. Множество, содержащее все элементы рассматривае-

мых множеств, называют универсальным множеством U.

Мощность (кардинальное число) множества A обозначается как ½A½. Для конечных множеств мощность – это число элементов. Например, ½Æ½ = 0, но í½ýÆ½ = 1.

Опр.6. Два множества A и B имеют одну и ту же мощность (или равномощны), если существует взаимно однозначное соответствие между этими множествами. Обозначают равномощность в виде ½A½ = ½B½.

Опр.7. Множество A есть бесконечное множество, если оно имеет ту же мощность, что и хотя бы одно из его собственных подмножеств; в противном случае A – конечное множество.

Множества, равномощные множеству натуральных чисел, называют счетными. Множества, равномощные множест-ву действительных чисел, называют континуальными.

Пример 2. К числовым множествам относятся: множество

натуральных чисел N; множество целых чисел Z; множество

рациональных чисел Q; множество иррациональных чисел

W; множество действительных чисел R. Множества N, Z, Q

– счетные, W, R – континуальные

Для описания множеств будем использовать два способа:

1. Перечисление: A = ía, b, cý; X = íx1, x2, ¼, xný.

2. Задание множества с помощью записи свойства,

определяющего отношение принадлежности элементов

данному множеству: Пример 3. A – множество студентов ЧелГУ.

Пример 4. C = [a, b] = íx: a £ x £ b, a Î R, b Î Rý - отрезок на множестве действительных чисел R.

A = íx: Q(x)ý - множеству А принадлежат все те и только те

элементы x, которые обладают свойством Q(x).

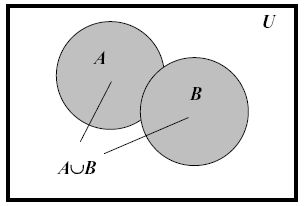
Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри него - кругов (или каких-либо других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств.

Введем список кратких обозначений: $ – существует, найдётся; " – любой; Û – тогда и только тогда, когда; Þ – следует; Î – принадлежит; Ì – содержится.

Операции над множествами

Объединением множеств A и B называется множество,

каждый элемент которого принадлежит хотя бы одному из

множеств A или B: A È B = íx: xÎA Ú xÎBý.

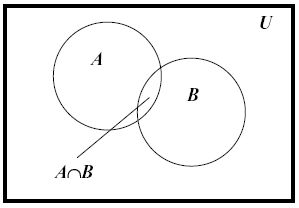
Пересечением множеств А и В называется множество, каждый элемент которого принадлежит одновременно и множеству А, и множеству В: A Ç B = íx: xÎA & xÎBý.