6.7.2. Метод а.М.Пирвердяна

Неустановившийся прямолинейно-параллельный фильтрационный поток, так же как и в предыдущем случае, разбивается на две области – возмущенную и невозмущенную. Однако в отличие от метода ПССС распределение давления в возмущенной области задается в виде квадратичной параболы, касательная к которой в точке горизонтальна. Это обеспечивает плавное смыкание профиля давлений в возмущенной и невозмущенной областях.

Рассмотрим два случая применительно к прямолинейно-параллельному потоку.

Характерис-тика потока	Случай I. Q=const	Случай II. Рг=const
Закон движения границы возму-щенной области
Дебит галереи
Закон распреде-ления давления в пласте	при ; при	при ; при

6.7.3. Метод интегральных соотношений

Метод предложен Г.И.Баренблаттом и основан на следующих предпосылках:

а) в каждый момент времени пласт делится на конечную возмущенную область и невозмущенную область, в которой движение отсутствует;

б) в возмущенной области распределение давления представляется в виде многочлена с коэффициентами, зависящими от времени;

Для прямолинейно-параллельного потока:

; (6.20)

Для плоскорадиального потока:

. (6.21)

Число членов n выбирается в зависимости от желаемой точности решения;

в) коэффициенты a₀, a₁,…,a_n , а также размер области возмущения l(t) или R(t) находятся из условий на галерее (забое скважины), из условий непрерывности и гладкости кривой давления на границе области возмущения, а также из особых интегральных соотношений.

Если принять в формуле (6.20) n=1, а в формуле (6.21) n=0, то получатся решения, соответствующие методу ПССС. Если n=2, то из метода интегральных соотношений вытекает как частный случай метод А.М.Пирвердяна.

Рассмотрим задачу плоскорадиальной неустановившейся фильтрации упругой жидкости к скважине радиусом R_c, пущенной в эксплуатацию в момент времени t=0 с постоянным дебитом Q. В начальный момент времени давление в пласте постоянно и равно Р_к.

Распределение давления в возмущенной области пласта зададим в виде:

Коэффициенты a₀, a₁ и a₂ определяются из условий на забой скважины и на границе возмущенной области.

Условие на забое:

при

На границе возмущенной области имеем:

при ,

при - условие гладкости кривой давления.

Тогда:

; ; .

При этом слагаемые, пропорциональные R_c или R_c², отброшены вследствие их малости.

После подстановки в формулу распределения давления будем иметь:

Закон движения границы возмущенной области:

.

6.7.4. Метод усреднения ю.Д Соколова-г.П.Гусейнова

Метод заключается в том, что в дифференциальном уравнении упругого режима

производная давления заменяется некоторой функцией времени F(t):

.

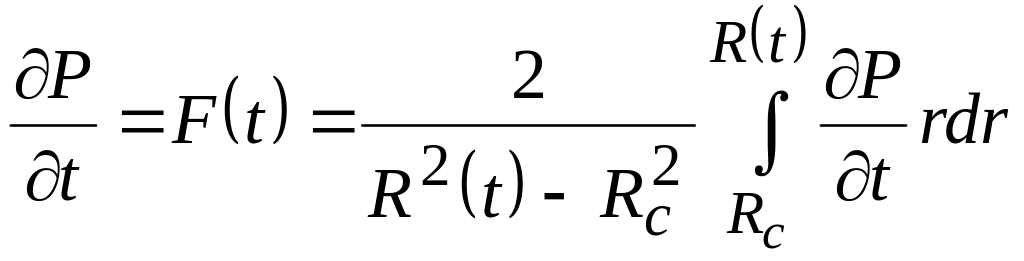Значение функции определяется из начальных и граничных условий.

После замены получаем:

.

Интегрируя данное уравнение по r и учитывая начальные и граничные условия, можно получить закон распределения давления в плоскорадиальном потоке при постоянном дебите скважины Q:

; .

Э.Б.Чекалюк предложил определять дебит скважин, работающей с постоянным забойным давлением, по формуле Дюпюи, введя в нее радиус возмущенной области:

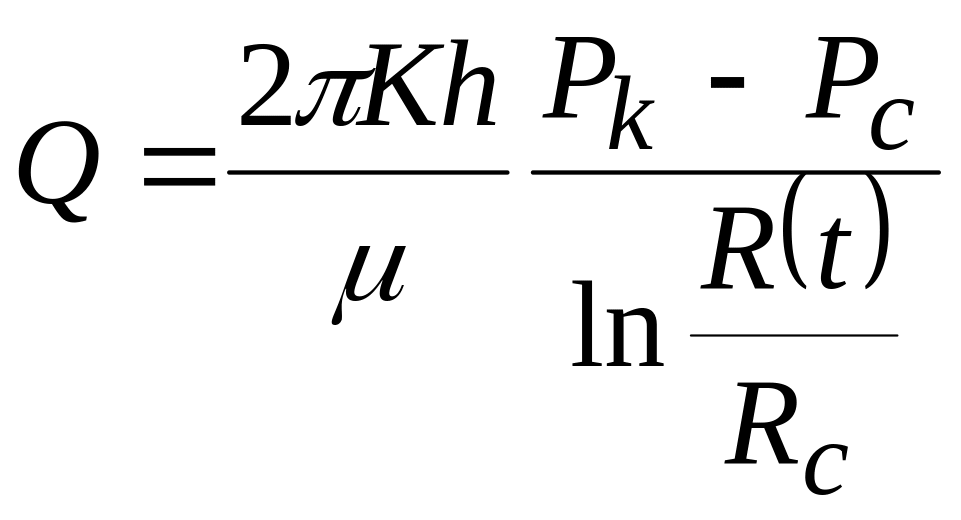, где .

Эта формула очень важна для практики. Относительная погрешность при определении дебита не превышает 1%.