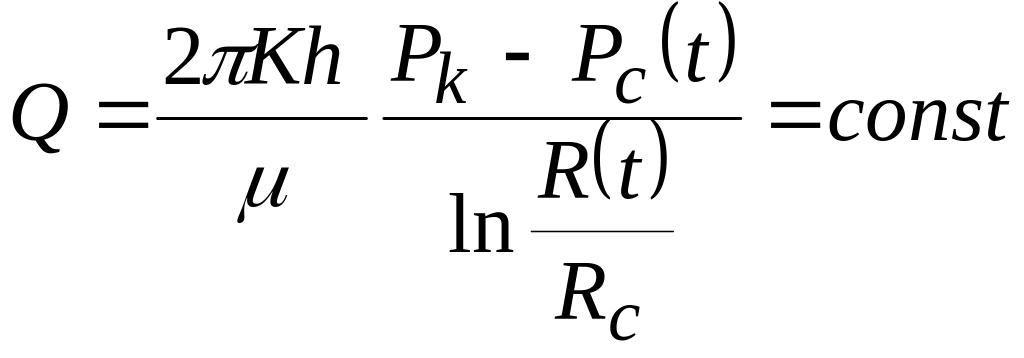6.6. Интерференция скважин в условиях упругого режима

При совместной работе в пласте нескольких добывающих и нагнетательных скважин изменения давления, вызванные работой каждой скважины, алгебраически суммируются по принципу суперпозиции. Скорости фильтрации в любой точке пласта суммируются геометрически.

Для расчета изменения пластового давления используется основная формула упругого режима. Хотя эта формула выведена для точечного стока в бесконечном пласте, В.Н.Щелкачев показал, что ею можно с высокой степенью точности пользоваться и в расчетах притока упругой жидкости к скважине конечного радиуса в открытом или закрытом конечном пласте.

(6.19)

где - изменение давления в произвольной точке пласта M; n – число скважин; Q_j – дебит j-ой скважины, причем Q_j>0, если скважина добывающая, и Q_j<0, если скважина нагнетательная; r_j – расстояние от центра j-ой скважины до точки М.

Если скважины начали работать в разное время, то формула (6.19) будет иметь вид:

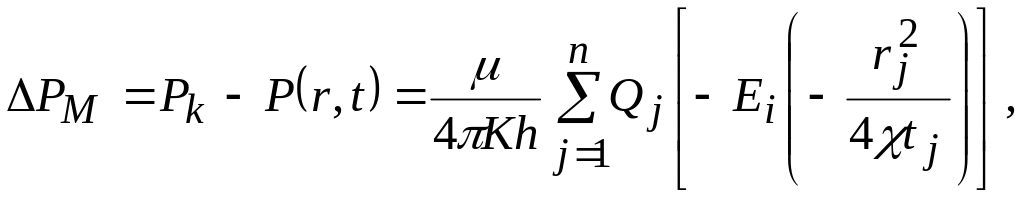
где t_j – время, прошедшее с начала работы j-ой скважины.

6.7. Приближенные методы решения задач теории упругого режима

Формулы (6.13), (6.16) и (6.18) представляют собой точные решения основного дифференциального уравнения упругого режима фильтрации, полученные путем интегрирования при заданных начальных и граничных условиях.

Однако существуют и приближенные решения, полученные с помощью различных методов. Наиболее известны:

метод последовательной смены стационарных состояний (ПССС);
метод А.М.Пирвердяна;
метод интегральных соотношений;
метод «усреднения» .

6.7.1. Метод последовательной смены стационарных состояний

Данный метод предложен И.А.Чарным и основан на предположении, что давление в пласте изменяется во времени значительно медленнее, чем по координате. Поэтому производную по времени можно в первом приближении отбросить, в результате чего для давления получается уравнения Лапласа, описывающее стационарный процесс.

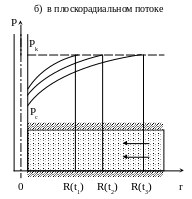
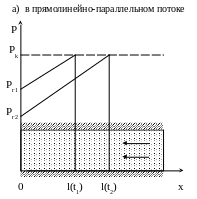
Рис. 6.1. Кривые распределения давления по методу ПССС

В каждый момент времени вся область движения жидкости условно разделяется на две области: возмущенную и невозмущенную. При этом предполагается, что в возмущенной области, начинающейся от стенки скважины, давление распределяется так, как будто бы движение жидкости в ней установившееся. Внешняя граница этой области служит в данный момент контуром питания. В невозмущенной области пласта давление всюду постоянно и равно начальному. Закон движения подвижной границы раздела двух областей определяется при помощи уравнения материального баланса и граничных условий.

Характерис-тика	Прямолинейно-параллельный поток	Плоскорадиальный поток
Случай I. Галерея (скважина) эксплуатируется с постоянным дебитом, Q=const
Распределение давления в воз-мущенной обла-сти	, 0  x  l(t)
Дебит галереи (скважины)
Закон движения границы возму-щенной области
Закон распреде-ления давления в целом по пла-сту	при ; при	при ; при
Случай II. На галерее (скважине) поддерживается постоянное давление
Дебит галереи (скважины)


Закон движения границы возму-щенной области		где - безразмерный радиус во-ронки депрессии, R(t)/R_c;  - безраз-мерное время
Распределение давления в пла-сте	при ; при	___________