2.3. Дифференциальные уравнения движения. Основное уравнение фильтрации. Закон Дарси для анизотропных сред

Закон Дарси записан в конечном виде, т.е. для пласта или образца породы с постоянной площадью сечения.

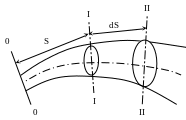
Для трубки тока с переменной площадью сечения закон Дарси запишется в дифференциальной форме:

. (2.4)

В проекциях на оси координат:

- дифференциальные уравнения движения

Если ось z направлена вертикально вверх, то дифференциальные уравнения движения примут вид:

. (2.5)

Определим из системы уравнений (2.5) производные , , :

После подстановки полученных значений в уравнение неразрывности (2.3’) получим:

,

откуда

. (2.6)

Уравнение (2.6) является дифференциальным уравнением установившейся фильтрации несжимаемой жидкости по закону Дарси в недеформируемой пористой среде и называется уравнением Лапласа.

Основное уравнение фильтрации выводится путем объединения уравнения неразрывности, уравнений движения и, если флюид сжимаем, уравнений состояния. В наиболее общем виде оно записывается в виде:

. (2.7)

Формула (2.4) справедлива для изотропной среды, для которой характерно постоянство проницаемости К по всем направлениям в окрестности рассматриваемой точки.

Пористые среды, в которых коэффициент проницаемости зависит от направления потока, называются анизотропными. Большинство пород-коллекторов имеют отчетливую слоистую структуру. Если плоскость xy совместить с плоскостью слоя, а координатную ось z направить перпендикулярно, то закон Дарси можно записать в виде:

дифференциальные уравнения движения для анизотропных сред

-

Здесь К – проницаемость параллельно напластованию; К_z – проницаемость перпендикулярно напластованию.

2.4. Уравнения состояния

Дифференциальные уравнения (2.3) и (2.5) содержат коэффициенты плотности  и вязкости  флюида, а также коэффициенты пористости m и проницаемости К породы. Зависимости этих параметров от давления называются уравнениями состояния флюида и пористой среды.

Параметр	Экспоненциальная зависимость	Линейная зависимость
Плотность
Вязкость
Пористость
Проницаемость

₀, ₀, m₀, К₀ – значения параметров при фиксированном (начальном давлении Р₀;

, , m, К – значения параметров при текущем давлении Р;

_ж – коэффициент объемного сжатия жидкости, Па^-1;

_с – коэффициент объемной упругости среды, Па^-1;

_, _m, _к – коэффициенты, определяемые экспериментально и зависящие от свойств жидкости и породы, Па^-1.

Уравнения состояния пласта и насыщающих его флюидов замыкают систему дифференциальных уравнений.

2.5. Начальные и граничные условия

Чтобы решить систему уравнений, необходимо задать начальные и граничные условия.

Начальное условие заключается в том, что задается искомая функция во всей области в некоторый момент времени, принимаемый за начальный.

Например, если искомой функцией является пластовое давление, то начальное условие может иметь вид:

Р=Р₀(x, y, z) при t=0,

т.е. в начальный момент времени задается распределение давления во всем пласте.

Если в начальный момент пласт невозмущен, то начальное условие принимает вид:

Р=Р₀=const при t=0.

Граничные условия задаются на границах пласта.

Продуктивный пласт или выделенную из него часть можно рассматривать как некоторую область пространства, ограниченную поверхностями – границами. Внешними границами являются кровля и подошва пласта, а также контур питания. Стенка скважины является внутренней границей пласта.

Число граничных условий должно быть равно порядку дифференциального уравнения по координатам.

Возможны следующие граничные условия.